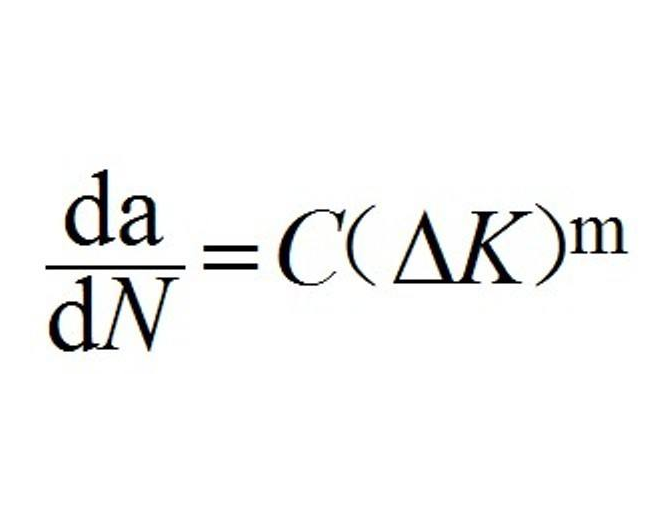基本介紹
- 中文名:帕里斯公式
- 外文名:paris formula
- 提出者:美國人帕里斯
- 提出時間:年1963
- 作用:估算裂紋擴展壽命
- 學科:力學
簡介,計算方法,帕里斯公式積分,
簡介
帕里斯認為裂紋尖端的應力場強度可以用應力強度因子K1來表示,那么就只有應力強度因子才是裂紋擴展的真正推動力,所以提出了直接與應力強度因子變化範圍ΔK有關的裂紋擴展公式。
如圖1所示,當裂紋前端的ΔK>ΔKth後,裂紋開始擴展,lg(da/dN)和lg(ΔK)呈線性關係,稱為疲勞裂紋擴展的第 I 階段。
當ΔK繼續增加,過來轉折點B1後,進入第 II 階段,擴展速度增長放慢,lg(da/dN)和lg(ΔK)仍是直線關係。當ΔK增大到超過第 II 階段轉折點B2,這時Kmax已接近材料的K1c,擴展速度急劇加快,直至斷裂。
由於 I 、II 階段在雙對數坐標中是直線,說明da/dN和ΔK之間存在指數關係,因此,帕里斯提出了如下的裂紋擴展速率的經驗公式
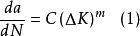
式中:
a —— 裂紋深度或寬度;
N —— 應力循環次數;
C、m —— 和材料有關的參數;
ΔK —— 應力強度因子變化範圍。
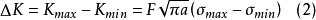
有人為了考慮平均應力影響,將r=Kmin/Kmax(循環特性)計入,此稱平均應力強度因子的影響參數。一般r增大,da/dN增大;同時考慮到Kmax趨近K1c時da/dN急劇增加的趨勢,建議用下式進行計算
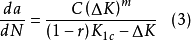
式中:K1c —— 斷裂韌性。
也有人將Kth計入,建議用下式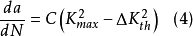
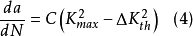
此式一般適用於疲勞裂紋擴展初期。
回到帕里斯公式,試驗表明,表中的材料常數C、m只有在第 II 階段時為常數。假定第 I 階段末,即B1點對應的裂紋長度為初始裂紋,以第 II 階段的帕里斯公式作為壽命管理的依據。
計算方法
用帕里斯公式計算裂紋擴展壽命(循環次數)時,先設一個裂紋的增量 Δa,計算相應的ΔK值,從而由帕里斯公式得ΔN1,然後在新的裂紋半長(a+ Δa)上再設一個增量 Δa,計算相應的ΔK,由公式得 ΔN2,這樣一直計算到所需要的數值為止。
帕里斯公式積分
從帕里斯公式積分,可以估算出裂紋擴展壽命。將式(4)帶入式(1),對N積分有
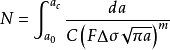
式中:
a0 —— 初始裂紋;
ac —— 臨界裂紋。
若將F作為常數處理,在等幅應力σa作用下(m≠2),則
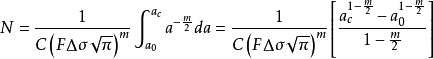
如果考慮F隨a變化,可分段處理,取每段F的較高值(偏安全),分段積分再加起來即得總N。