定義
斷裂韌性表征材料阻止裂紋擴展的能力,是
度量材料的韌性好壞的一個定量指標。在載入速度和溫度一定的條件下,對某種材料而言它是一個常數,它和裂紋本身的大小、形狀及外加應力大小無關,是材料固有的特性,只與材料本身、熱處理及加工工藝有關。當裂紋尺寸一定時,材料的斷裂韌性值愈大,其裂紋失穩擴展所需的臨界應力就愈大;當給定外力時,若材料的斷裂韌性值愈高,其裂紋達到失穩擴展時的臨界尺寸就愈大。它是應力強度因子的臨界值。常用斷裂前物體吸收的能量或外界對物體所作的功表示。例如應力-應變曲線下的面積。韌性材料因具有大的斷裂伸長值,所以有較大的斷裂韌性,而脆性材料一般斷裂韌性較小。
斷裂韌性在工程中受到重視的原因是,它表征與光滑試樣中強度特性完全相反的特性。例如,很粗略地說,同一系列的材料的斷裂韌性值隨屈服強度增加而下降。因此,儘管按屈服強度準則認為已進行十分安全設計的高強度材料的結構,由於其構件中某種原因或有缺陷或產生裂紋,甚至也會發生不穩定斷裂造成致命的損傷。由於材料屈服強度隨溫度下降而增大,在設計過程中未考慮低溫斷裂韌性的情形,也會造成同樣結果。過去結構物斷裂事故中,由於對上述斷裂韌性認識不足而發生的事故一定不少。
一般地說,在不穩定斷裂之先,隨著載荷增加斷裂徐徐進行,即所謂穩定斷裂的情形不少。雖是一種穩定斷裂,但由於疲勞,應力腐蝕裂紋,蠕變等原因,裂紋擴展後轉變為不穩定斷裂的情形也不少。
如把臨界缺陷擴展稱為不穩定斷裂,把亞臨界缺陷擴展叫做穩定斷裂,不管穩定斷裂的內容如何,斷裂韌性均表示材料在穩定斷裂轉變為不穩定斷裂時的阻抗值。當然,斷裂韌性受事先進行的穩定斷裂的影響是明顯的。同時,我們知道斷裂韌性值有顯著的尺寸效應。尺寸效應是產生應力狀態和屈服範圍問題的原因,尤其是屈服範圍構成選擇表示斷裂韌性的力等參數問題。
影響因素
如能提高斷裂韌性,就能提高材料的抗脆斷能力。因此必須了解斷裂韌性是受哪些因素控制的。影響斷裂韌性的高低,有外部因素,也有內部因素。
外部因素
外部因素包括板材或構件截面的尺寸、服役條件下的溫度和應變速率等。
材料的斷裂韌性隨著板材或構件截面尺寸的增加而逐漸減小,最後趨於一穩定的最低值,即平面應變斷裂韌性KIC。這是一個從平面應力狀態向平面應變狀態的轉化過程。
斷裂韌性隨溫度的變化關係和衝擊韌性的變化相類似。隨著溫度的降低,斷裂韌性可以有一急劇降低的溫度範圍,低於此溫度範圍,斷裂韌性趨於一數值很低的下平台,溫度再降低也不大改變了。
關於材料在高溫下的斷裂韌性,Hahn和Rosenfied提出了以下經驗公式:
式中: n——高溫下材料的應變硬化指數;E——高溫下材料的彈性模量,MPa;
σs——高溫下材料的屈服應力,MPa;
Ψ——高溫下單向拉伸時的斷面收縮率。
應變速率的影響和溫度的影響相似。增加應變速率和降低溫度的影響是一致的。
內部因素
內部因素有材料成分和內部組織。作為材料成分與內部組織因素的綜合,材料強度是一巨觀表現。從力學上而不是冶金學的角度,人們總是首先從材料的強度變化出發來探討斷裂韌性的高低。只要知道材料強度,就可大致推斷材料的斷裂韌性。下圖為AISI 4340(40CrNiMo)鋼的斷裂韌性和經淬火、回火熱處理成不同屈服強度後的相互關係。可見,斷裂韌性是隨材料屈服強度的降低而不斷升高的。這一試驗結果是有代表性的,大多數低合金鋼均有此變化規律。即使像馬氏體時效鋼(18Ni)也是如此,只不過同樣強度下斷裂韌性值較高些而已。
 KIC和屈服強度的關係
KIC和屈服強度的關係斷裂韌性結果
在斷裂韌性的測定中,有三個階段,在第一階段里,FPZ逐漸形成,應力強度因子KI值將會單調增加;在第二階段里,裂紋發生穩定擴展;然後在第三階段,出現了KI值的突然減少到KIC值。對於這種現象的一種可能解釋是數值方法的固有假定所至。在有限元標定中假定了理想的線彈性系統,但隨著實驗的進行,此假定卻進一步失去正確性。因為有限裂紋長度增加,可以觀察到大的殘餘CMOD。這個影響,在實驗開始時可以忽略,但到實驗的後期此影響是相當大的。
一般地,僅僅第二階段時的斷裂韌性值可以作為靜力分析時用。它們的平均值總結於下表中。從表中,我們可以觀察到如下現象:
①上面的表中所列的相對偏差都在範圍20%以內,斷裂韌性的客觀值與試件的尺寸無關,並可以獲得;
②基於水平方向上的相對誤差,也可發現斷裂韌性與MSA的尺寸無關;
③這些結果是在無限制條件的實驗室里得到的,對於限制應力對斷裂韌性的影響可見1990年Saouma等人的研究結果。
測試方法
壓痕法
測試試樣表面先拋光成鏡面,在顯微硬度儀上,以10Kg負載在
拋光表面用硬度計的錐形金剛石壓頭產生一壓痕,這樣在壓痕的四個頂點就產生了預製裂紋。根據壓痕載荷P和壓痕裂紋擴展長度C計算出斷裂韌性數值(KIC)。 計算公式為:
,其中E為
楊氏模量,例如對於Si3N4系統一般取300GPa。公式中載荷P單位為N,裂紋長度C單位為mm,顯微硬度HV單位為GPa。
 壓痕法實例圖
壓痕法實例圖試樣類型
目前國內常用的斷裂韌性試樣有兩種:
1)三點彎曲試樣SE(B);
2)緊湊拉伸試樣C(T)。
 SENB
SENB試驗方法
在試樣中間開一裂紋,通過三點或四點抗彎斷裂測試,計算材料的斷裂韌性。
測試方法比較
①IM法比SENB法簡便經濟,但測得的數據不如SENB法可靠;
②SENB法是普遍公認的標準測試方法;
③為了實際方便,要對IM法測試公式修正,使結果更接近SENB法。
工程套用
金屬材料的斷裂韌性、裂紋擴展速率和裂紋擴展的門檻值等力學性能指標已為廣大的力學測試、材料研究和金相專家所了解,並已在零部件的強度設計、新材料的研製、材料的套用研究、材料強度規律的試驗研究、熱處理工藝的選擇以及失效分析中得到了廣泛的套用。本文的目的,是圍繞斷裂韌性的“基本原理”和“工程套用”這兩個方面,為力學、材料和金相專家們提供更全面、更深入的內容,以便在今後的試驗研究和工程套用中發揮更大的效益。
金屬材料的平面應變斷裂韌性KIC,是在斷裂力學這門學科形成後提煉出來的一個新型的力學性能指標。而早期斷裂力學的誕生則是研究防止脆性破壞的結果,因此,我們還得先談一點有關脆性破壞的情況。
脆性破壞是機械零件失效的重要方式之一。它是在零件受載過程中,在沒有產生明顯巨觀塑性變形的情況下,突然發生的一種破壞。由於事先沒有明顯的跡象,所以脆性破壞的危險性很大。
防止零部件發生脆性破壞的傳統方法是:
①要求選用的材料具有一定的塑性指標δ和Ψ,並具有一定的衝擊韌性Ak值。這種選材方法完全是根據零部件的使用經驗來定的,它既沒有充足的理論根據,又不能保證零部件工作的安全性。例如,1950年美國北極星飛彈固體燃料發動機殼體在實驗發射時,發生了爆炸事故,而所使用的1373MPa屈服強度的D6AC鋼是經過嚴格檢驗的:其塑性和衝擊韌性指標都是完全合格的。又如,我國生產的120T氧氣頂吹轉爐的轉軸也曾經發生過斷軸事故,而所使用的40Cr鋼的強度、塑性和衝擊韌性指標都是經過檢驗而達到設計要求的。
②採用轉變溫度的方法,對材料的轉變溫度提出一定的要求。由於現在的一次沖斷試驗,只考慮了應力集中和加大應變速率這兩個因素,還沒有考慮溫度降低對材料脆性破壞的影響。為此,設計了系列衝擊試驗,即在一系列不同溫度下進行衝擊試驗,得到Ak-T曲線和脆性斷口百分率-溫度T的曲線,由此確定脆性斷口轉變溫度,常用的是FATT50。一般認為,只要零部件的實際工作溫度大於材料的脆性轉變FAATT50,就不會發生脆性破壞。
儘管如此,上面兩種方法都還是經驗性的,它們無法找到實驗室中的轉變溫度與實際零部件的轉變溫度之間的轉換關係。因此,按這種方法的設計和選材,要么很保守,要么照樣產生脆性破壞。國內外大量的軸、轉子、容器和管道、焊接結構出現的大量脆性破壞事故表明,傳統的防斷方法必須改變。
試驗研究表明,大量的低應力脆性破壞的發生,是和零件內部存在巨觀缺陷有關的。這些缺陷有的是在生產過程中產生的,如在冶煉、鑄造、鍛造、熱處理和焊接中產生的夾雜、氣孔、疏鬆、白點、摺疊、裂紋和未焊透等;有的是在使用過程中產生的,如疲勞裂紋、應力腐蝕裂紋和蠕變裂紋等。所有這些巨觀缺陷,在斷裂力學中都被假設(抽象化)為裂紋,在零部件承受外載入荷時,裂紋尖端產生應力集中。如果材料的塑性性能很好,它就能使裂紋尖端的集中應力得到充分的鬆弛,這就可能避免脆性開裂。但是.如果由於某些原因:或是材料的塑性性能很差;或是零件尺寸很大,約束了材料的變形;或是工作溫度的降低,使材料工作在轉變溫度以下;或是載入速率的提高,使材料塑性變形跟不上而呈脆性;或是腐蝕介質或射線輻照的作用引起材料的脆化等等,就有可能使裂紋尖端產生脆性開裂,從而造成零件的脆性破壞。
當帶缺陷的物體受力時,研究其內部缺陷——裂紋附屬檔案近應力應變場情況及其變化規律,研究裂紋開裂的條件,以及裂紋在交變載荷下的擴展規律等內容,就形成了一門新的學科——
斷裂力學。
研究進展
隨著機率斷裂力學工程套用的逐步深入,材料斷裂韌性分散性問題,已成為影響含缺陷結構機率安全評定的關鍵因素之一。合理解決材料斷裂韌性分散性是一個十分複雜的問題。一方面由於冶金過程等方面的偏差,造成材料斷裂韌性的分散性;另一方面由於試樣幾何尺寸、裂紋
長度測量等
試驗誤差,亦會導致測試結果的不確定性,還有不同測試規範和標準對測試數據的處理也會導致測試結果的不確定性。若缺陷位於焊接部位,影響因素將更加複雜。除上述原因外,還會有諸如焊接上藝、焊材、以及不同操作人員及焊後熱處理等因素導致斷裂韌性測試結果分散性更加嚴重。儘管分析和解決其分散性問題如此複雜,十分困難,然而,在對含缺陷焊接結構(尤其是工業鍋爐、壓力容器和管道)進行安全評定時,重點就是焊接接頭區而不是母材。如何處理斷裂韌性的分散性問題已成為工程界不可迴避的問題,也是機率安全評定應解決的基本問題之—。
對材料斷裂韌性
分散性規律的研究,在理論和實踐上均已取得較大進展。
Hauge和Thualow分別採用Weibull分布、LogNormal分布、Slather模型以及Neville模型,對兩組CTOD數據(86個母材和16個焊材)進行了統計分析,其主要結論如下:
①兩組CTOD數據並非服從形狀參數為2的Weibull分布(或Slather模型);雙參數Weibull分布、LogNormal分布和Neville分布都適宜
擬合這些數據。
②90%置信限的中位期望值可較好地由LogNormal分布得到;對於只有三個子樣時,能較好地等效於三個值十取最小值的方法;對大子樣,LogNormal吻合更好。
③對於小子樣,LogNormal分布提供最為可靠的估計,Weibull分布和Neville模型在於樣為3和5時由於數據不夠,難以估計分布參數值。
④數值模擬結果及
擬合結果均表明LogNormal分布無論對太子樣還是小於樣,擬合精度足夠,不是特別保守。
Mimura等對由於材料不均勻而引起斷裂韌性的分散性做了分析與試驗研究。經過從同一塊板上取樣的CharpyV型試塊試驗分析,提出了區別材料不均勻性導致的分散性與測試中導致的分散性的方法。


 KIC和屈服強度的關係
KIC和屈服強度的關係
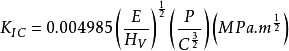
 壓痕法實例圖
壓痕法實例圖 SENB
SENB
