基本介紹
- 中文名:希臘拉丁方
- 外文名:Graeco-Latin square
- 別稱:正交拉丁方
- 所屬學科:數學(統計學)
- 性質:試驗設計的一種
- 簡介:由兩個互相正交的拉丁方重疊而成
基本介紹
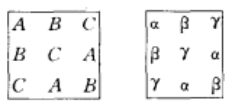 圖1
圖1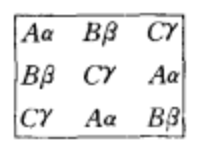 圖2
圖2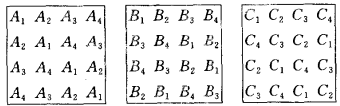 圖3
圖3

希臘拉丁方設計
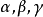
 圖4
圖4










來源 | 自由度 | 平方和 |
行 | k-1 |  |
列 | k-1 |  |
拉丁字母 | k-1 |  |
希臘字母 | k-1 |  |
殘差 | (k-3)(k-1) | 由減法得到 |
總計 | k2-1 | 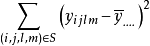 |

 圖1
圖1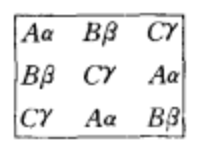 圖2
圖2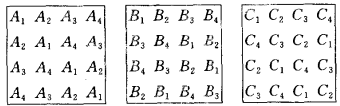 圖3
圖3

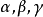
 圖4
圖4










來源 | 自由度 | 平方和 |
行 | k-1 |  |
列 | k-1 |  |
拉丁字母 | k-1 |  |
希臘字母 | k-1 |  |
殘差 | (k-3)(k-1) | 由減法得到 |
總計 | k2-1 | 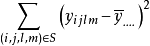 |
希臘拉丁方亦稱“正交拉丁方”,試驗設計的一種。由兩個互相正交的拉丁方重疊而成。本質上可以與正交表互變。三階希臘拉丁方可用於四因子,每個因子各有三個水平的...
超希臘-拉丁方,即拉丁方陣(英語:Latin square),是一種 n × n 的方陣,在這種 n × n 的方陣里,恰有 n 種不同的元素,每一種不同的元素在同一行或同一...
正交拉丁方設計是使用正交拉丁方安排的一種試驗方案,當存在m個相互正交的n階拉丁方時,用拉丁方的行和列分別表示兩個因素的n個水平,用這m個拉丁方的記號分別表示...
5.1拉丁方簡介 5.2拉丁方設計的原理 5.3拉丁方設計的試驗布置 5.3.1單拉丁方設計的試驗布置 5.3.2多拉丁方設計的試驗布置 5.3.3希臘—拉丁方設...
多種平衡方法以消除疲勞效應,其中主要有對抗平衡法(ABBA法——是指每一種實驗條件都以正反兩種順序呈現給被試)、全隨機法、區內隨機法、拉丁方和希臘拉丁方設計...
第五章拉丁方設計與分析 第一節拉丁方設計簡介 一、拉丁方設計 二、重複拉丁方設計 三、堯敦方設計 四、希臘拉丁方設計 第二節拉丁方設計的實施及SAS...
Graeco-Latin square, 希臘拉丁方Grand mean, 總均值Gross errors, 重大錯誤Gross-error sensitivity, 大錯敏感度Group averages, 分組平均...
3.1.4 希臘拉丁方設計 3.2 兩因子試驗設計及其方差分析 3.2.1 完全隨機設計 3.2.2 隨機區組設計 3.2.3 拉丁方設計 3.3 三因子試驗設計及其方差...
第5節 拉丁方設計及其資料的統計分析第6節 不完全拉丁方設計及其資料的統計分析第7節 希臘拉丁方設計及其資料的統計分析第8節 析因設計及其資料的統計分析...
第一節 拉丁方設計一、原理二、拉丁方試驗結果的分析示例第二節 希臘拉丁方設計一、原理二、希臘拉丁方試驗結果的分析示例思考與習題...
4.4 多個分區組成分:拉丁方設計4.5 平衡不完全區組設計附錄4A 圖形方差分析的基礎附錄4B 一些有用的拉丁方:希臘拉丁方和超希臘拉丁方設計第5章 兩水平因析設計...
