布爾方程(Boolean equation)是一類特殊方程,指布爾代數B上含有未知元的等式f(X)=g(X),其中f(X)與g(X)均為B上之布爾函式。當X=(x1,x2,…,xe)時,稱此方程為e元布爾方程,而稱x1,x2,…,xe為未知元。若有a1,a2,…,ae∈B使之f(a1,a2,…,ae)=g(a1,a2,…,ae),則稱(a1,a2,…,ae)為e元布爾方程的一個解。對於具有形狀h(X)=0或h(X)=1的布爾方程,稱為0-1布爾方程,可以證明:形如f(X)=g(X)的布爾方程均可化為等價的0-1布爾方程。解0-1布爾方程的一個可行方法是逐次消元法,對於布爾函式中僅含0與1為其常量的0-1布爾方程有三種解法:即分項求解法、分支解法及卡諾圖解法,求解布爾方程不僅具有理論意義,而且在計算機科學及電路設計中均有重要套用,對於布爾方程x+y=a+b顯然有一解: x=a,y=b。
基本介紹
- 中文名:布爾方程
- 外文名:Boolean equation
- 所屬學科:數學
- 特例:0-1布爾方程
定義
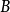
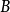
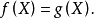
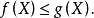
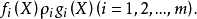
0-1布爾方程
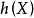
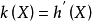

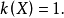
1元布爾方程
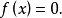
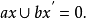
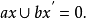
重要定理
定理1
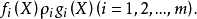
定理2
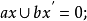
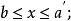
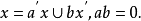
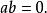
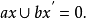
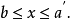
定理3