韋布爾模型

威布爾模量是一個無量綱參數的威布爾分布用於描述變化測量脆性材料的材料強度

基本介紹

• 中文名：韋布爾模型
• 產生背景：陶瓷等脆性材料的最大應力,
• 測試分析：測量了許多小樣本的脆性陶瓷材料
• 相關：DIN EN 843 - 5和DIN 51 110 - 3

產生背景

陶瓷等脆性材料的最大應力,可以測量樣品能夠承受失敗可能會有所不同,從標本之前,即使在相同的測試條件。這是有關物理缺陷的分布在表面或身體脆弱的標本,從脆性破壞過程產生在這些弱點。缺陷是一致的和均勻分布時,樣品將會表現得更加均勻比缺陷集中分布不一致。

這必須考慮當描述材料的強度,所以力量是最好的代表值的分布,而不是作為一個特定的值。威布爾模數是形狀參數威布爾分布模型,在這種情況下,地圖組件的失效機率在不同壓力。

測試分析

考慮強度測量了許多小樣本的脆性陶瓷材料。如果測量顯示不同樣本小變化,計算威布爾模量將會很高,一個強度值作為描述sample-to-sample性能好。可能得出的結論是,它的物理缺陷,無論是內在產生的材料本身或製造過程中,均勻的分布在整個材料。如果測量顯示高變化,威布爾模數計算將低;這表明缺陷集中不一致和實測強度將整體疲軟和變數。產品由組件的低威布爾模數將表現出低可靠性和自己的優勢廣泛分布。
指定測試程式確定威布爾模數在DIN EN 843 - 5和DIN 51 110 - 3。

如果強度的機率分布,X,威布爾分布的密度

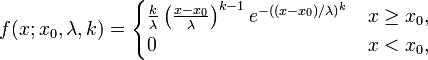
k是威布爾模數。

韋布爾模型：(Weibull model) 按章節查詢 按名稱查詢

韋布爾模型又稱韋布爾機率密度函式(Weibull probability density function)，在工業上廣泛套用於電子產品的壽命檢測等，彭尼帕克(Pennypacker 1980)引入植病流行學用於季節流行動態的描述。其微分式為：

(4.19)積分形式為: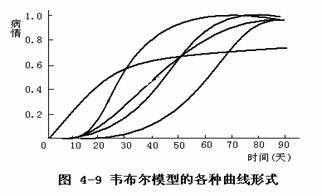

(b>0,c>0,t>a) (4.20)

式中：t為時間；a為位置參數，表示病害開始增長的時間；x為時間t時刻病情(以小數表示)；b為比率參數，與病害增長速率呈負相關；c為曲線的形狀參數，也與流行速度有關。

由於該模型有a、b、c三個參數，各參數的種種組合可描述多種形式的流行曲線(圖4.9)，故與理察模型相似，均屬彈性模型(flexible model)。當c=1時，韋布爾方程可用來描述單利病害的增長。當c=3.6時，曲線的拐點在x=0.5處出現，曲線是中心對稱的，此時韋布爾函式與邏輯斯蒂函式基本一致，只是各個時期的增長速度快慢與三個參數的取值有關。

方程(4.20)也可改寫成直線形式：

(4.21)

方程4.21的截距為-clnb，斜率為c，由於方程(4.21)有三個參數,在不知道病害始發期的情況下，無法用最小二乘法擬合。但我們可以不斷假設a值建立回歸方程並比較它們的擬合度。也就是用“逼近法”或疊代法推算這三個參數（參考肖悅岩，1985）。而由此推算出來的始病期更為可信