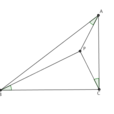
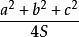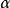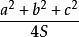已知三角形ABC,P是內部一點,若角PAB=角PBC=角PCA=角α,則P為布洛卡點,角α為布洛卡角.
基本介紹
- 中文名:布洛卡點
- 外文名:Brocard's point
- 別稱:勃羅卡點
- 套用學科:數學
- 適用領域範圍:平面幾何
提出背景,基本原理,
提出背景
實際上布羅卡爾點早在1816年就已被法國數學家和數學教育家克雷爾(A.L.Crelle,1780—1855)首次發現。
克雷爾曾是德國柏林科學院院士和彼得堡科學院通訊院士,他於1826年創辦《純粹與套用數學雜誌》,對數學的發展起過重要作用。他本人對幾何學有較高造詣,關於三角形性質發表過研究成果,其中包括“布羅卡爾點”的發現。但是他的發現並未被當時的人們所注意。
1875年,三角形這一特殊點,被一個數學愛好者——法國軍官布羅卡爾(Brocard,1845—1922)重新發現,並用他的名字命名。這才引起萊莫恩、圖克(Tucker,1832—1905)等一大批數學家的興趣,一時形成了一股研究“三角形幾何”的熱潮。據有人統計,在1875~1895這20年中,有關此方面的著述竟達600種之多。其間不少新的結果,都與布羅卡爾的名字聯繫在一起,因而有“布羅卡爾幾何”一說的流傳。
基本原理
布洛卡點,也叫“勃羅卡點”,定義為:已知P為ABC內一點,若角PAB=角PBC=角PCA=角α,則P為布洛卡點,角α為布洛卡角.一般地,對於任意三角形都有兩個布羅卡爾角與兩個布羅卡爾點,當三角形為正三角形時,兩個布羅卡爾角重合。
已知P為三角形ABC的一個布羅卡爾點,相應的布羅卡爾角是∠PAB=∠PBC=∠PCA=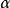 ,則
,則
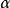
cot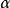 =cotA+cotB+cotC=
=cotA+cotB+cotC=