基本介紹
- 中文名:巴爾末公式
- 外文名:balmer formula
- 別稱:Balmer公式
- 提出者:巴爾末(J.J.Balmer)
- 提出時間:1885年
- 套用學科:化學 物理
- 適用領域範圍:光譜
- 作用:表示氫原子譜線波長
定義
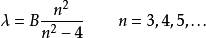
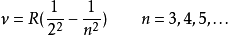



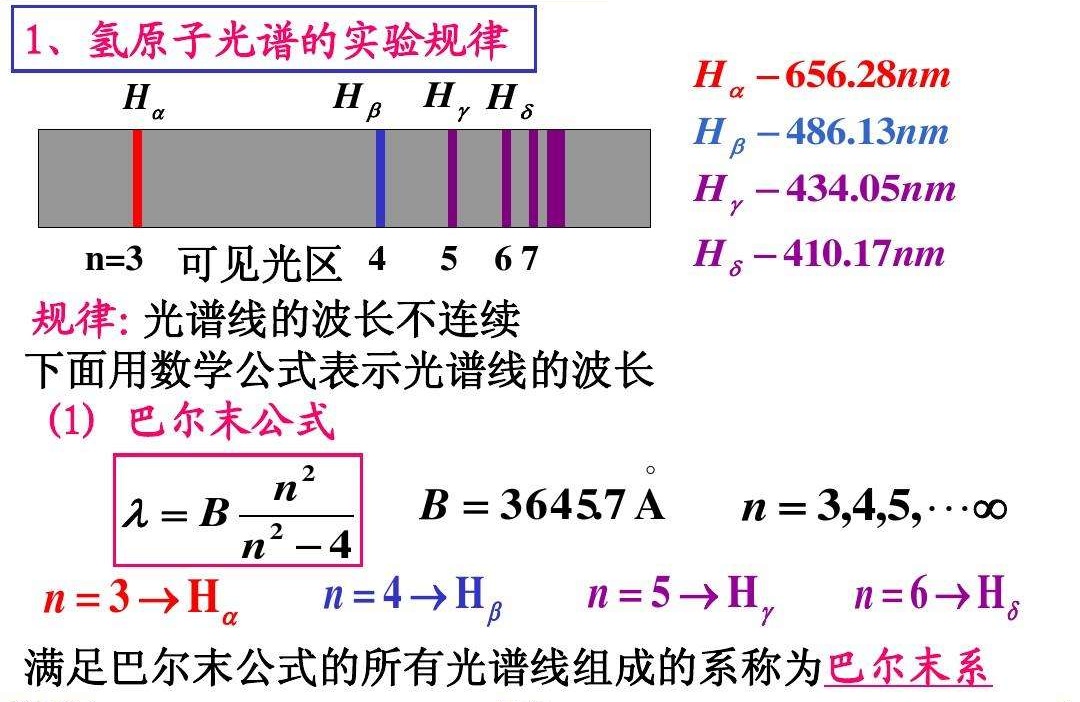
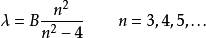
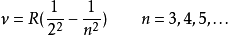



巴爾末公式(Balmer公式)是1885年由瑞士數學教師巴爾末(J.J.Balmer)提出的用於表示氫原子譜線波長的經驗公式。又稱作Balmer公式。...
1885年由瑞士數學教師巴爾末提出的用於表示氫原子譜線波長的經驗公式 ...... 提出巴爾末公式 1885年由瑞士數學教師巴爾末提出的用於表示氫原子譜線波長的經驗公式 :...
約翰·雅各布·巴耳末(Johann Jakob Balmer)瑞士數學家、物理學家。 主要貢獻是建立了氫原子光譜波長的經驗公式——巴耳末公式。為紀念巴耳末,月球表面的一個...
根據巴爾末公式1/λ=R(1/m2-1/n2),其中R=1.0974×107m-1。其中,當m=1, n=2,3,4...時,該公式所表示的是躍遷到基態的譜線,即萊曼系。萊曼系是...
玻爾的原子結構模型取得了巨大的成功,較好地了解決原子的穩定性問題,並且成功地解釋了氫光譜的巴爾末公式,對氫原子和尖氫離子光譜的波長分布規律作出了完滿的解釋,...
里德伯計算氫氣能級公式波數1/λvac = R (1/m^2 - 1/n^2 )(JJ.Balmer提出的巴爾末公式轉換為波數形式)其中λvac是溢出真空中的電磁波波長...
——對電磁場不對稱性的思考 3.11 結晶體 3.12 二氧化矽結晶螺旋線上分子自然序數分布與巴爾末公式 3.13 光量子在太陽引力場內偏轉和水星近日點的進動 3.14 ...
現代科學理論,如電磁場結構理論,愛因斯坦的廣義相對論引力場方程乃至未成功的統一場論,巴爾末公式,量子力學矩陣方程,分子生物學大分子立體結構理論等,皆與上述人文...
19世紀末20世紀初,物理學處於新舊交替的時期。生產的發展和技術的提高,導致了物理...特別是關於黑體輻射的實驗規律,運用經典理論得出的瑞利-金斯公式,雖然在低頻部分...
