巴拿赫-薩克斯性質

巴拿赫-薩克斯性質是關於點列的算術平均值收斂的一個重要性質。若巴拿赫空間X有巴拿赫-薩克斯性質，則它必有弱巴拿赫-薩克斯性質。

基本介紹

• 中文名：巴拿赫-薩克斯性質
• 外文名：Banach-Saks property
• 適用範圍：數理科學

簡介

巴拿赫-薩克斯性質是關於點列的算術平均值收斂的一個重要性質。

若巴拿赫空間X中的每個有界點列{x_n}有一子列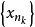，使它的算術平均值按範數收斂於X中的一個元x₀，即

則X稱為具有巴拿赫-薩克斯性質。

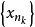
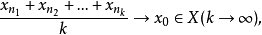
弱巴拿赫-薩克斯性質

若X中每個弱收斂的點列{x_n}有一子列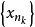,使它的算術平均值按範數收斂於X中的一個元x₀，則X稱為具有弱巴拿赫-薩克斯性質。

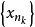
推論

由巴拿赫-薩克斯性質的定義可知以下結論成立：

1.若巴拿赫空間X有巴拿赫-薩克斯性質，則它必有弱巴拿赫-薩克斯性質。

2.若巴拿赫空間X是超自反的，則X必有巴拿赫-薩克斯性質。

3.若巴拿赫空間X具有巴拿赫-薩克斯性質，則X必是自反的。這是尼西烏拉(Nishiura,T.)和瓦特曼(Waterman,D.)於1963年證明的；伯恩施坦(Bernstein,A.R.)於1972年指出，逆命題並不成立。