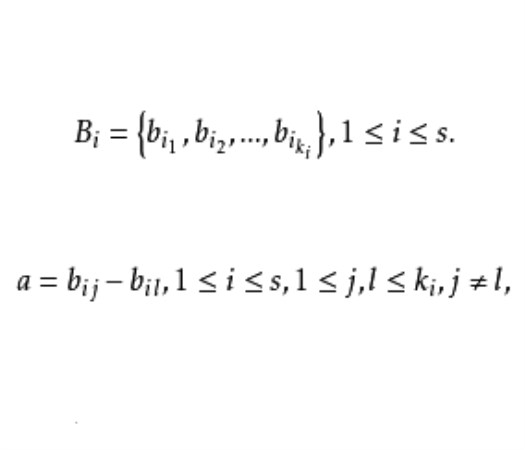差族(difference family)是組合設計的一種工具,用於構作BIBD設計或PBD,設B1,B2,…,Bs是v階群G的子集,運算以加法表示,Bi={bi1,bi2,…,biki},K={ki|1≤i≤s},若G中每個非零元在所有的差bij-bil(1≤i≤s)中恰出現λ次,則稱B={B1,B2,…,Bs}是一個(v,K,λ)差族。
基本介紹
- 中文名:差族
- 外文名:difference family
- 所屬學科:數學
- 所屬問題:組合學(組合設計)
- 簡介:用於構作BIBD設計或PBD
基本介紹,相關定理,
基本介紹
差族概念是差集概念的自然推廣。差族方法是構作各類設計的最常用也是最有效的方法之一。
定義1 設G為v階Abel群,其運算為加法,設s為正整數,K為由正整數組成的集合,再設S為由G的s個子集 組成的子集族。此處
組成的子集族。此處


(i)G中任意非零元a都恰有λ次表成如下形式的差:
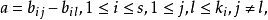
(ii)當1≤i≤s時都有

則稱S為G中的一個(v,K,λ)-差族(difference family)。當G=Zv為v階循環群時,S叫做(v,K,λ)-循環差族。當K={k}時,S叫做(v,k,λ)-差族。
若:
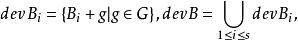

補差集和 補差集可用來構作4v階的阿達馬矩陣,若
補差集可用來構作4v階的阿達馬矩陣,若 為一個
為一個 補差集,且滿足條件:x∈D1就有x-1
補差集,且滿足條件:x∈D1就有x-1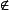 D1,則稱{D1,D2}為采克勒斯差集。從一個采克勒斯差集可得到一個
D1,則稱{D1,D2}為采克勒斯差集。從一個采克勒斯差集可得到一個 階反型阿達馬矩陣,當2m+1滿足以下條件之一時存在采克勒斯差集:
階反型阿達馬矩陣,當2m+1滿足以下條件之一時存在采克勒斯差集: 為素數冪;2m+1≡5(mod 8)且2m+1為素數冪;m=4n,2m+1=pt,p為素數,p≡5(mod 8)且t≡2(mod 4)。
為素數冪;2m+1≡5(mod 8)且2m+1為素數冪;m=4n,2m+1=pt,p為素數,p≡5(mod 8)且t≡2(mod 4)。



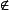


相關定理
引理1 設G為v階Abel群, 為G的s個子集,若對1≤i≤s都有
為G的s個子集,若對1≤i≤s都有 。則子集族S={
。則子集族S={ ]為G中(v,K,λ)-差族的充分必要條件是
]為G中(v,K,λ)-差族的充分必要條件是



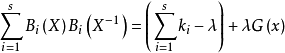
對1≤i≤s,將由Bi中元素作成的差的全體所組成的多重集記作ΔBi。即

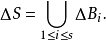
定理1 設G為v階加法Abel群,S為G中的一個(v,K,λ)-差族。則(G,DevS)是一個B(K,λ;v)。
定理2 若存在(v,k,λ)-差族。則
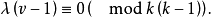
引理2 若存在v階Abel群G中的(v,k,λ1)-差族與(v,k,λ2)-差族。則存在G中的(v,k,λ1+λ2)-差族;特別,若(v,k,λ)-差族存在。則對任一整數t,(v,k,tλ)-差族也存在。