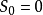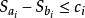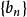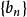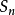如果一個系統由n個變數和m個約束條件組成,形成m個形如ai-aj≤k的不等式(i,j∈[1,n],k為常數),則稱其為差分約束系統(system of difference constraints)。亦即,差分約束系統是求解關於一組變數的特殊不等式組的方法。
基本介紹
- 中文名:差分約束系統
- 外文名:system of difference constraints
- 標籤:信息學技術
求解差分約束系統,可以轉化成圖論的單源最短路徑(或最長路徑)問題。
觀察xj-xi<=bk,會發現它類似最短路中的三角不等式d[v]<=d[u]+w[u,v],即d[v]-d[u]<=w[u,v]。因此,以每個變數xi為結點,對於約束條件xj-xi<=bk,連線一條邊(i,j),邊權為bk。我們再增加一個源點s,s與所有定點相連,邊權均為0。對這個圖,以s為源點運行Bellman-ford算法(或SPFA算法),最終{d[ i]}即為一組可行解。
例如,考慮這樣一個問題,尋找一個5維向量x=(xi)以滿足:
這一問題等價於找出未知量xi,i=1,2,…,5,滿足下列8個差分約束條件:x1-x2≤0
x1-x5≤-1
x2-x5≤1
x3-x1≤5
x4-x1≤4
x4-x3≤-1
x5-x3≤-3
x5-x4≤-3
該問題的一個解為x=(-5,-3,0,-1,-4),另一個解y=(0,2,5,4,1),這2個解是有聯繫的:y中的每個元素比x中相應的元素大5。
引理:設x=(x1,x2,…,xn)是差分約束系統Ax≤b的一個解,d為任意常數。則x+d=(x1+d,x2+d,…,xn+d)也是該系統Ax≤b的一個解。
bellman-ford算法偽代碼:
for each v V do d[v] <-- 無限大; d[s] <-- 0
Relaxation
for i =1,...,|V|-1 do
for each edge (u,v) 屬於 E do
d[v] <-- min{d[v], d[u]+w(u,v)}
Negative cycle checking
for each v 屬於V do if d[v]> d[u] + w(u,v) then no solution
在實際的套用中,一般使用SPFA(Shortest Path Fast Algorithm)算法來實現。
差分約束系統中源點到每個點的距離確定
關於Dist[]的初始化化
1.如果將源點到各點的距離初始化為0,最終求出的最短路滿足 它們之間相互最接近了
2.如果將源點到各點的距離初始化為INF(無窮大),其中之1為0,最終求出的最短路滿足 它們與該點之間相互差值最大。
3.差分約束系統的確立要根據自己確定的約束條件,從約束點走向被約束點
連邊一般有兩種方法,第一種是連邊後求最長路的方法,第二種是連邊後求最短路的方法。
例:d[x]-d[y]>=Z
如果想連邊後求最長路 那么將不等式變形為這種形式 d[x]>=d[y]+z y---x連一條權值為z的邊
求最短路則變形成d[y]<=d[x]-z x---y連一條權值為-z的邊。
如果是別的不等式,也可以根據情況變形。但是要保證的是 兩個變數(x,y)的係數一定要是正的。而常量則不一定。
定理:將如上差分約束系統 轉換成圖後,以
轉換成圖後,以 為源點得到的最短路徑序列為
為源點得到的最短路徑序列為 (如果有解),則
(如果有解),則 滿足
滿足 且若
且若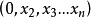 為
為 任意解,則有
任意解,則有 。
。







證明:首先由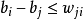 ,則顯然有
,則顯然有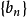 滿足
滿足 ,這是因為每條邊對應一個不等式且由圖的構造法可知。其次考察
,這是因為每條邊對應一個不等式且由圖的構造法可知。其次考察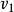 到
到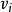 的最短路徑
的最短路徑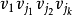 ,我們有
,我們有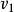 與
與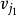 直接相連且由路徑最短知
直接相連且由路徑最短知 ,其中
,其中 為不等式
為不等式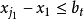 的常量即為邊
的常量即為邊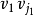 的權,所以有
的權,所以有 。對k做歸納,由
。對k做歸納,由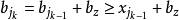 ,又
,又 ,所以
,所以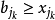 即
即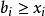 所以後者成立。證畢
所以後者成立。證畢
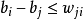
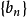

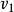
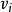
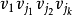
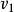
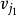


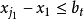
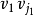

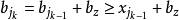

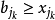
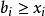
例:設有n個盒子標號為1...n,每個盒子最多放1個球。放法滿足 (0<i≤m)約束,其中
(0<i≤m)約束,其中 表示區間
表示區間 最多可放
最多可放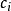 個球,求這n個盒子最多可放多少個球。
個球,求這n個盒子最多可放多少個球。



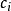
令前k個盒子放的數目為 ,則有
,則有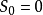 ,
, (1 ≤ i ≤ n ),
(1 ≤ i ≤ n ),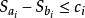 (1 ≤ i ≤ m)。以此約束條件用如上算法給出最短路徑序列
(1 ≤ i ≤ m)。以此約束條件用如上算法給出最短路徑序列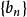 ,由定理知
,由定理知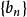 是合法的放法,且
是合法的放法,且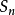 為最大值。
為最大值。