基本介紹
- 中文名:導網叢
- 外文名:jet bundle
- 所屬學科:數學
- 簡介:奇點理論的一個重要概念
基本介紹,相關介紹,
基本介紹
1.

2.任意選取點p與點 的局部坐標系,對於選取的局部坐標系,f和g的所有階≤k的導數在點p的值都對應地相等。
的局部坐標系,對於選取的局部坐標系,f和g的所有階≤k的導數在點p的值都對應地相等。

這個條件與點p和點 的局部坐標系的選取無關,常以記號
的局部坐標系的選取無關,常以記號 記f與g在p點k階等價,於是,k階等價是一個等價關係,考慮映射集合
記f與g在p點k階等價,於是,k階等價是一個等價關係,考慮映射集合


{ ,f無窮次可微},
,f無窮次可微},

這個集合在k階等價這個等價關係下分成一些等價類, 由這些等價類做成的空間記為 ,若
,若







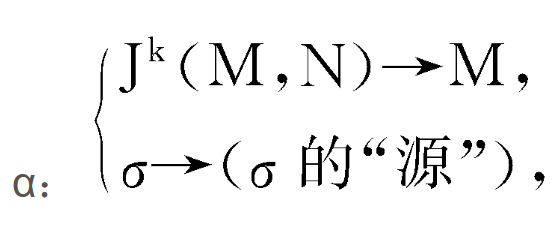
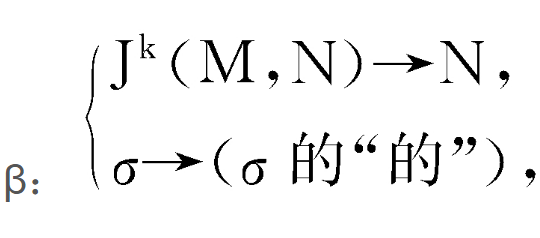
稱α為源映射,β為的映射,從而, 是一纖維叢,稱
是一纖維叢,稱 為M×N上的k階導網叢,而且
為M×N上的k階導網叢,而且 也是微分流形。
也是微分流形。



相關介紹
k階導網映射(k-jet mapping)是一種特殊的映射,是由給定的映射導出的到導網空間的映射。是指:對給定的映射f,對其定義域上的每個點,對應f在該點的k階導網。設M,N是微分流形, 是無窮次可微映射,可以定義從M到導網叢空間
是無窮次可微映射,可以定義從M到導網叢空間 的映射
的映射 如下:
如下:








稱映射 為映射f的k階導網映射,f的k階導網映射
為映射f的k階導網映射,f的k階導網映射 仍為無窮次可微映射。
仍為無窮次可微映射。