基本介紹
術語解釋
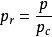


性質

分類
絕對壓力
臨界壓力
原理









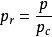












對比壓力是實際氣體無因次的重要基本對比狀態參數之一。其值等於氣體所處實際狀態下的絕對壓力與其臨界壓力的比值。...
自然界中的各種物質都存在臨界狀態,此時其液態的比體積與氣態比體積相同。臨界狀態的狀態參數稱臨界參數,如臨界壓力、臨界比體積、臨界溫度,分別用pc、vc、Tc表示。...
對比態原理又稱對應態原理,不同物質如果具有相同的對比壓力pr(壓力p與臨界壓力pc之比)和對比溫度Tr(溫度T與臨界溫度Tc之比),就是處於對應態,這時它們的各種物理...
對比密度是實際氣體無因次的重要基本對比狀態參數之一。其值等於氣體所處實際狀態下的密度與其臨界密度的比值。...
對比狀態定率又稱對應狀態定律二該定律可表述為:不同種實際氣體處於相同的對比溫度T和對比壓力p時,必具有相同的對比體積v。當不同的實際氣體處於相同的 r戶和v時...
reduced variables 實際氣體的對比溫度(reduced temperature)Tr、對比壓力(reduced pressure)pr、對比體積(reduced volume) Vr的總稱。三者分別定義為Tr=T/Tc, pr=p...
對比狀態方程redured eyua}ion }F state採用無因次的 對比變數來描述實際氣體平衡狀態的方程式。無因次的對比 變數指的是對比壓力h*- h}h},}"f比TFm度Tr_...
物理學上的壓力,是指發生在兩個物體的接觸表面的作用力,或者是氣體對於固體和液體表面的垂直作用力,或者是液體對於固體表面的垂直作用力。習慣上,在力學和多數工程...
詞目:對比體積 釋文:。指1摩爾真實氣體在壓力P、溫度T的體積Vm與該氣體臨界壓力、臨界溫度下的體積Vc之比,以Vr表示。其公式表達式為 Vr=Vm /Vc ...
公稱壓力PN(0.1MPa):與管道系統部件耐壓能力有關的參考數值,為便於使用,通常取R10系列的優先數。公稱壓力是指管材在二級溫度(20℃)時輸水的工作壓力。若水溫在...
對比溫度是實際氣體無因次的重要基本對比狀態參數之一。其值等於氣體所處實際狀態下的絕對溫度與其臨界溫度的比值。...
職業壓力即指不同職業者和不同職位者在工作中所受到的壓力。2010年12月,某課題組公布其壓力調查的研究結果,研究發現,領導層級越高,心身健康水平相對越低。...
傳統上所謂壓力測試(stress testing)是指將整個金融機構或資產組合置於某一特定的(主觀想像的)極端市場情況下,如假設利率驟升100個基本點,某一貨幣突然貶值30%,股價...
標準溫度和壓力英文名稱為standard temperature and pressure,簡稱STP,也是所謂的標準狀況(標準狀態),簡稱“標況”。由於地表各處的溫度、壓強皆不同,即使是同一地點...
有效壓力,系土骨架所承擔的壓力,使顆粒彼此靠攏,導致土發生壓縮變形並提高土的抗剪強度。它是土中兩種壓力形態之一。在地應力比較高的地區,潛在的能量具備突然釋放...
壓力和體位性多汗是指體位改變和側臥位時一側身體受壓所產生的出汗反應,是多汗症的一種表現。多汗症是由於交感神經過度興奮引起汗腺過多分泌的一種疾病。...
壓力與應對(華中科技大學研究生課程教材)...... 圖集 壓力與應對圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:5次歷史版本 最近更新: 創建者:jxNO77VI...
通過測試了解自己現在目前的的壓力程度,以及了解自己性格的好壞程度...... A型性格較之B型性格,對壓力更敏感,也比較容易過激,對壓力的心理承受能力也差一些。因此A型...
《壓力與健康》是中國社會出版社出版的圖書,作者是姬天舒,邵艷梅。...... 《壓力與健康》闡述了壓力對健康的一般問題,並提供了正確對待壓力 的原則和方法,通俗易...
《與壓力同行》是2011年華文出版社出版的圖書,作者是萬軾。本書是一本教會現代職場人士如何在壓力下快樂工作,化壓力為動力,從而實現自身良好職業發展的指導用書。...
《心理壓力與健康》是2006年華東師範大學出版社出版的圖書,作者是耿興永...... 《心理壓力與健康》是2006年華東師範大學出版社出版的圖書,作者是耿興永 ...
Siege是一個壓力測試和評測工具,用於WEB開發。...... Siege是一個壓力測試和評測工具,設計用於WEB開發這評估套用在壓力下的承受能力:可以根據配置對一個WEB站點進行...
《心理壓力與應對策略》是2007年浙江大學出版社出版的圖書,作者是趙國秋。...... 《心理壓力與應對策略》是2007年浙江大學出版社出版的圖書,作者是趙國秋。...
