對數級數(logarithmic series)，即對數函式的冪級數展開式。
基本介紹
- 中文名：對數級數
- 外文名：logarithmic series
- 定義：對數函式的冪級數展開式
這個級數由梅卡托(Mercator, N.)發表於1668年出版的《對數級數》中，故又稱梅卡托級數.
對數級數
相關詞條
- 對數級數
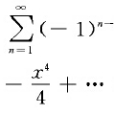
對數級數(logarithmic series)，即對數函式的冪級數展開式。這個級數由梅卡托(Mercator, N.)發表於1668年出版的《對數級數》中，故又稱梅卡托級數....
- 對數分布
對數分布(logarithmic distribution)可以指兩個意思：①即“對數級數分布”。②稱隨機變數X有對數分布，參數為n(自然數)，如果P{X=m}=log(1+1/m),(m=1,2,...,n-1)。對數級數分布 對數級數分布亦稱對數分布，是負二項分布的極限形式。稱隨機變數X服從參數為 的對數級數分布，如果 此分布的機率，恰好是...
- 費希爾對數級數
費希爾對數級數 費希爾對數級數是2013年公布的海峽兩岸生態學名詞。 公布時間 2013年全國科學技術名詞審定委員會審定公布的海峽兩岸生態學名詞。出處 《海峽兩岸生態學名詞》。
- 自然對數
展開並逐項積分，得到了自然對數的無窮級數。“自然對數”最早描述見於尼古拉斯·麥卡托在1668年出版的著作《Logarithmotechnia》中，他也獨立發現了同樣的級數，即自然對數的麥卡托級數。大約1730年，歐拉定義互為逆函式的指數函式和自然對數。大名鼎鼎的牛頓後來也研究過對數。現在的對數記號是大數學家歐拉在 1748年引入...
- 二元對數分布
二元對數分布 二元對數分布亦稱二元對數級數分布。
- 對數函式
“log”是拉丁文logarithm（對數）的縮寫，讀作：[英][lɔɡ][美][lɔɡ, lɑɡ]。簡介 對數函式是6類基本初等函式之一。其中對數的定義：如果a=N（a>0，且a≠1），那么數x叫做以a為底N的對數，記作x=logₐN，讀作以a為底N的對數，其中a叫做對數的底數，N叫做真數。一般地，函式y=logₐx...
- 對數積分
由於這個積分在x趨近於0時，值會趨近於負無窮大，有些數學家為了避免麻煩，常會選擇另外一個相似的定義，歐拉對數積分定義為：或 函式li(x)有一個正根，它出現在x≈ 1.45136 92348 ...。這個數稱為Ramanujan-Soldner常數。其中 是不完全伽瑪函式。級數表示法 函式li(x)與指數積分Ei(x)有以下的關係：其中x>...
- 電機極對數
P就是極對數。極數確定 八極電機就是轉子有8個磁極，2p=8,即此電機有4對磁極。一般汽輪發電機多為隱極式電機，極對數很少，一般為1、2對，而n=60f/p,所以他的轉速很高，最高可達3000轉（工頻），而水輪發電機的極數相當多，轉子結構為凸極式，工藝比較複雜，由於他的極數很多，所以它的轉速很低，可能只有...
- 對數判別法
第一對數判別法：若存在p，使n充分大時 或等價地，Lₙ>1，則∑aₙ收斂；若n充分大時Lₙ≤1，則∑aₙ發散。第二對數判別法：設Lₙ=|ln(1/(naₙ))|/lnln n，結論同上。對數判別法的證明 設 ，且 ，試證明：當0 發散；當A>1時，級數 收斂。分析 該命題是正項級數的一個判斂法，稱為...
- 三角函式對數表
三角函式對數表是一種常用的數據表，指具有一定間隔的銳角三角函式值的常用對數值表。如正弦對數表、餘弦對數表、正切對數表、餘切對數表，常見有4位、5位(中學生用)和6—10位(工程和科研用)的三角函式對數表。由於正弦函式與餘弦函式，正切函式與餘切函式在[0°，90°]內互余，所以造表時常把正弦對數和餘弦對數...
- 墨卡托級數
在數學內，墨卡托級數(Mercator series)或者牛頓-墨卡托級數(Newton–Mercator series)是一個自然對數的泰勒級數。介紹 在數學內，墨卡托級數(Mercator series)或者牛頓-墨卡托級數(Newton–Mercator series)是一個自然對數的泰勒級數：使用大寫sigma表示則為 當 −1 歷史 這級數被尼古拉斯·墨卡托，牛頓和Gregory Saint-...
- 十位對數表
《十位對數表》是1974年科學出版社出版圖書，作者是沈時悅。內容簡介 本表採用因子法編排，列l兩個表．N各取了4位．本表內插採用冪級數展開的方法，不僅使表的篇幅大為減少，而且不需要藉助其他計算工具，即可求取對數值或真數值．本表可供工程技術人員、科研工作者、大專院校理工科師生作計算工具．圖書目錄 目錄...
- 對數簡法
《對數簡法(Duishu jianfa)》是清戴煦撰數學書，是《求表捷術》中的一種，二卷及續一卷，成書於1845年。該書主要內容是關於對數函式的冪級數展開及對數表的造法。藉助有理指數的二項式定理，得到了由開方表求對數、由自然對數求常用對數、由展開式求對數以及由三角函式的對數展開式造三角函式對數表等方法，從而...
- 種數-個體數關係
如果總種數為S，總個體數為N，從最低位第r項來看，在樣品數少的情況下，等比級數法則、對數級數法則、對數正規法則、負二項分布法則等，每一種均適用；但如果樣品數增多則前兩種法則的適用性有不太適宜的傾向。就多數群落來看，在真正個體數、順次排列與各項法則之間，恐怕存在著圖2所示的關係。另外，MacArthur的...
- 初等函式
一個初等函式，除了可以用初等解析式表示以外，往往還有其他表示形式。例如 ，三角函式 y=sinx 可以用無窮級數表為y=x-x³/3!+x⁵/5!-…初等函式是最先被研究的一類函式，它與人類的生產和生活密切相關，並且套用廣泛。為了方便，人們編制了各種函式表，如平方表、開方表、對數表、三角函式表等。有理函式 ...
- 生物多樣性(生態學術語)
2.對數級數分布：在一個或少數幾個生態因子占主導地位的群落中，物種在群落中的出現呈富集種很少，而稀有種很多的格局，物種多度分布較好地服從對數級數分布，群落中物種總數即S=α[-ln(1-x)]，群落中個體總數N=α/(1--x)，α與群落中物種數目和個體總數均成正比，且不受樣方大小的影響，是合適的群落多樣性...
- 基本初等函式
高等數學將基本初等函式歸為五類：冪函式、指數函式、對數函式、三角函式、反三角函式。數學分析將基本初等函式歸為六類：冪函式、指數函式、對數函式、三角函式、反三角函式、常數函式。下面一一介紹這些函式。冪函式 定義 一般地，形如y=x（有理數）的函式，即以底數為自變數，冪為因變數，指數為常數的函式稱為冪...
- 生態系統多樣性
綜合大多數學者的分析結果，物種豐富度指數（S），Shannon-Wiener指數（H）、Simpson指數、對數級數分布參數a和群落均勻度指數，是套用較為廣泛和值得推薦的幾種生態系統多樣性測度指標。當然，根據研究目的不同可以選擇更具針對性的測度方法。此外，在許多情況下物種多度分布模型，比單一的多樣性指數提供更好生態系統多樣...
- 高中代數學
第三章級數 第八編排列，組合，二項定理，或然率 第一章排列 第二章組合 第三章二項定理 第四章指數級數和對數級數 第五章或然率 第九編方程論 第一章方程通性 第二章根與係數的關係，根的對稱函式 第三章方程的變易 第四章虛根，笛卡特氏符號律 第五章無理根 第六章重根 第十編無窮級數 第一章收斂...
- 漢譯范氏大代數
xx等差級數 xxi等比級數 xxii調和級數 xxiii逐差法·高級等差級數·插入法 xxiv對數 xxv排列及組合 xxvi多項式定理 xxvii適遇法 xxviii算學歸納法 xxix方程論 xxx三次方程及四次方程 xxxi行列式及消去法 xxxii無窮級數之收斂 xxxiii無窮級數之演算 xxxiv二項級數，指數級數，對數級數 xxxv循環級數 xxxvi無窮連乘積 xxx...
- 物種多樣性指數
例如，當群落的物種多度服從對數級數時，它有2個參數α和x。其中X是樣本大小的函式，而另一個參數α不受樣本大小的影響，反映了群落的固有特性，因此，Fisher等將其定義為多樣性指數。然而，通過理論分布的參數去測度群落物種多樣性的方法有很大的局限性。首先，某些理論分布的參數與樣本大小有關，不適於作為多樣性...
- 江恩螺旋四方形
所以江恩四方形所計算的支撐及阻力位，其實是以8、16、24...為單位的數學級數。那奇序列 江恩四方形與黃金螺旋四方形都是從一個中心開始，以螺旋形態向外擴展開來，不同的是江恩四方形以等差級數增長，而黃金螺旋是以對數級數進行，其倍數單位為黃金分割比率1.618倍。江恩四方形與黃金螺旋四方形的阻力與支持位，有...
- 江恩四方形
江恩螺旋四方形之所以有著較準確的預測功能是因為它與黃金展開線有異曲同工之妙。不同的是，黃金展開線是以對數級數展開，後面一項是前一項的1.618倍，而江恩螺旋四方形是以算術級數展開，為等差數列。製作規則 江恩價格四方形主要用於分析價位的支持和阻力位。其製作方法比較特別，在製作四方形之前，我們必須首先確定...
- 范氏高等代數學
xx等差級數 xxi等比級數 xxii調和級數 xxiii遞差法.高階等差級數.插值法 xxiv對數 xxv排列及配合 xxvi多項定理 xxvii或然率 xxviii算學的歸納法 xxix方程式論 xxx普偏之三次及四次方程式 xxxi行列式及消去法 xxxii無窮級數之收斂 xxxiii無窮級數之算法 xxxiv二項級數，指數級數及對數級數 xxxv循環級數 xxxvi無窮連...
- 江恩測市工具
江恩螺旋四方形之所以有著較準確的預測功能是因為它與黃金展開線有異曲同工之妙。不同的是，黃金展開線是以對數級數展開，後面一項是前一項的1.618倍，而江恩螺旋四方形是以算術級數展開，為等差數列。江恩認為：1 一個升勢若以對角線上的價位為起點，則可能在價格的二次方上結束；2 一個跌勢若以對角線上的...
- 自然常數
自然常數，符號e，為數學中一個常數，是一個無限不循環小數，且為超越數，其值約為2.718281828459045。它是自然對數函式的底數。有時稱它為歐拉數（Euler number），以瑞士數學家歐拉命名；也有個較鮮見的名字——納皮爾常數，以紀念蘇格蘭數學家約翰·納皮爾（John Napier）引進對數。它就像圓周率π和虛數單位i，是...
- 新中華高中代數學
187．對數連級數 188．模數的求法 189．常用對數的求法 190．補算法原理 第十四章排配分析．或然率 191．本章研究的問題 192．基本問題同原則 193．求_nP_r法 194．關於排列的問題 195．物件不盡相異的排列 196．求_nC_r法 197．關於配合的定理 198．重複配合法 199．實際的例題 200．或然率 201．近真...
- 高中代數學(全一冊)
187．對數連級數 188．模數的求法 189．常用對數的求法 190．補算法原理 第十四章排配分析．或然率 191．本章研究的問題 192．基本問題同原則 193．求_nP_r法 194．關於排列的問題 195．物件不盡相異的排列 196．求_nC_r法 197．關於配合的定理 198．重複配合法 199．實際的例題 200．或然率 201．近真...
- 戴煦
著有《對數簡法》、《四元玉鑒細草》等。學術簡介 學術成就 戴煦在研究無窮級數時發現了“開方求對數”的簡便方法，並在此基礎上補充了“定理級對數”和“自然對數級數術”兩項定理，比當時世界上的先進算法要簡單實用得多。著作影響 戴煦一生論著頗多，除了《重差圖說》外，還著有《對數簡法》、《續對數簡法》...
