對抗解釋結構模型

Adversarial Interpretive Structure Modeling Method（簡稱 AISM）是在經典的解釋結構模型（ISM）基礎上，融入生成對抗網路（GAN）中的博弈對抗（Adversarial）思想，最新提出的一種模型方法。一言以蔽之AISM就是在不損失系統功能的前提下，通過相反的層級抽取規則，得出一對最簡的層次化的拓撲圖。

並且根據成對的層級拓撲圖進行釋意。

基本介紹

• 中文名：對抗解釋結構模型
• 外文名：Adversarial Interpretive Structure ModelingMethod
  AISM
• 適用領域：系統科學，系統工程
• 所屬學科：人工智慧、數學，管理

簡介

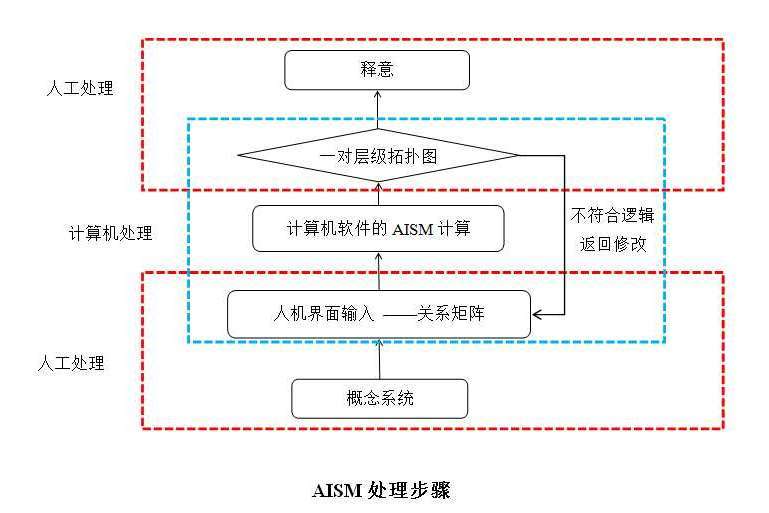
AISM是2020年新提出的一種方法，它源自於博弈解釋結構模型，其核心是在ISM結果優先的層級抽取規則的基礎上，加入與之對立的原因優先的層級抽取規則，從而建立一組對抗的層級拓撲圖。這種成對的拓撲層級圖的方式來解釋要素優劣（因果）排序的方法稱之為對抗解釋結構模型（AISM）。

相較於文字、表格、數學符號等方式，AISM在結果呈現上非常直觀且清晰，它把要素（評價對象、方案、樣本）看成一個結點，將存在因果（優劣、可達）關係的結點用有向線段標識，AISM最終以有向拓撲層級圖的方式呈現結點間的因果（優劣、可達）關係，進而很容易得出評價對象的優劣。習慣上把越優的結點放置於上面的層級，越劣的結點放置在越下的層級，最終按照層級的高低給出各個結點的排序，最上層的結點為最優集，最下層的為最劣集。層級從下至上形成由劣到優的排序系列。

需要特別指出的是通過結果（優要素）優先與原因（劣要素）優先層級抽取的方式，得到的有向拓撲層級圖可能並不一致。這種不一致恰好是觀察研究的重點。

同一般的解釋結構模型（ISM）對結果的解釋不同點在於，AISM更關注的是處於不同層級的要素。基於這些要素有如下定義。

在有向拓撲層級圖中，若某個要素處於不同的拓撲層級，則稱這個要素為活動要素（Activity elements）。

具有活動要素的系統稱之為可拓變系統（Extension variable system），也叫活動系統或拓撲活動系統。

不含活動要素的系統稱之為剛性系統（Rigid system），也叫拓撲剛性系統（Topological rigid system）。

在剛性系統中存在著一類完全剛性系統（Completely rigid system）。

完全剛性系統具有如下三個特性。

其一，關係矩陣中的要素從小到大排序後形成上三角矩陣的滿陣形式，即對角線右上方全為1，對角線左下方全為0；同理，關係矩陣中的要素從大到小排列後，則形成下三角矩陣的滿陣形式。

其二，兩種有向拓撲層級圖的結果是一致的，展現為直鏈型。

其三，任意兩個評價對象（樣本，要素，方案）之間都有確定的比較關係（優劣，好壞，可達，大小）。

成對拓撲層級圖的性質

第一、拓撲序方向一致

• 有向線段的屬性具有一致性。如有向線段的指向代表從差到好，代表從劣到優，代表從原因到結果。儘量不要出現某些有向線段的意思是從差到好，而另外的有向線段代表的是從原因到到結果。
• 習慣上發出有向線段的要素為劣要素，或者原因要素；接受有向線段的要素為優要素，結果要素。即從下到上是從劣到優；從原因到結果。

第二、層級數相同且最少

• 一組對抗的拓撲層級圖中，兩者的層級數目是一致的。

• 相較於拓撲排序得到的層級圖，AISM得到的拓撲層級圖的數目是最少的。它屬於緊湊結構，或者稱之為緊。

第三、線段最少即以一般性骨架矩陣代替

一般性骨架矩陣詳情請參見解釋結構模型的核心運算。

第四、迴路以最簡菊花鏈形式表達

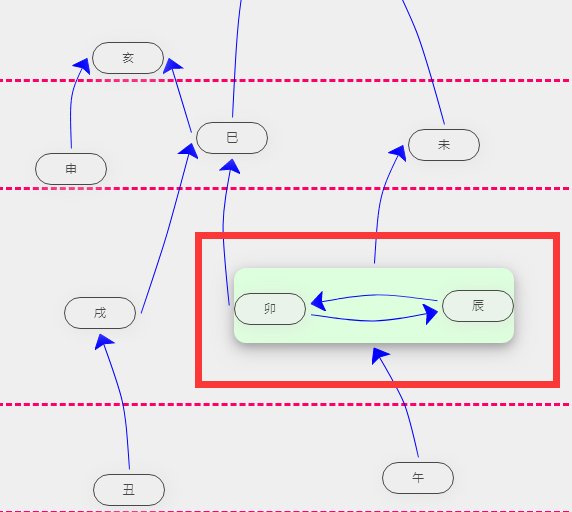
圖1 迴路畫法示意

、

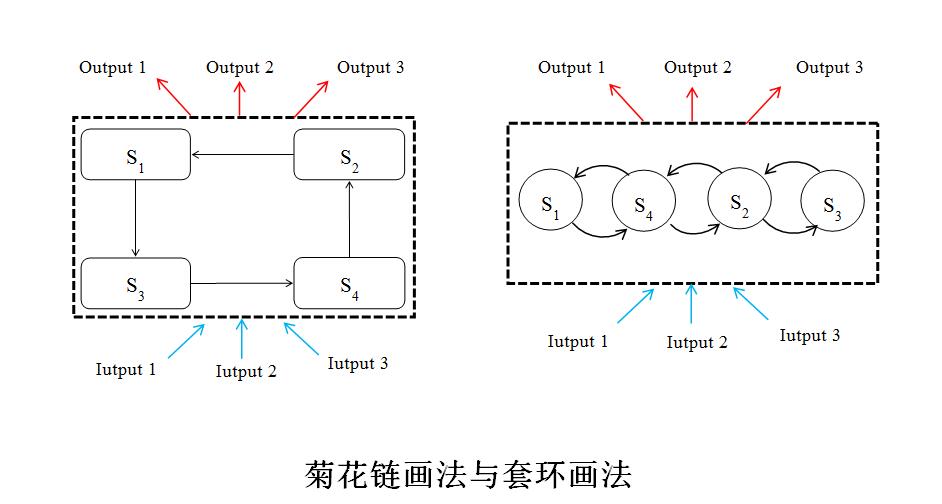
圖2 迴路菊花鏈畫法與套環畫法

菊花鏈畫法即以任意一條迴路代表強連通子集的畫法。

兩類運用的計算過程

1第一類、優劣、好壞比較排序類運用

計算過程為：

D：決策矩陣，評價矩陣，即有n行，m列的矩陣。n代表要素（評價對象，方案，樣本，樣品）m代表屬性（維度，評價準則，決策項，指標……）

A：關係矩陣，為n×n的布爾方陣。

其中 為最核心的一步

對於D中的每一列都具有嚴格的可比性。

對於含有m列的評價矩陣D，其中的任意一列即指標維度，具有同屬性，可比較的前提。維度的這種優劣的比較至少有著兩種屬性。

數值越大越優，數值越小越差，稱之為正向指標。記作p1、p2……pm。 數值越小越好，數值越大越差，稱之為負向指標。記作q1、q2……qm。

對於決策矩陣D中的任意兩行x,y

負向指標有且同時有

正向指標有

符合上述規則，要素x與要素y的偏序關係記作：

的意義為y要素優於(好於)x要素

上述規則成為偏序規則。對於決策矩陣通過偏序規則可以得到關係矩陣 A

由決策矩陣到關係矩陣算例見算例部分。

第二類、因果、可達邏輯排序類運用

其中：

A：關係矩陣，為布爾方陣。

I：單位矩陣，即主對角線全部為1的矩陣。

B：相乘矩陣，即主對角線填充1以後的布爾矩陣

R：可達矩陣，即B一直乘下去，不再變化後得到的矩陣稱之為可達矩陣

對於布爾方陣，有可達集合 R，先行集合 Q，共同集合 T，其中T = R ∩ Q。

以關係矩陣 A 為例，對於其要素：

的可達集合記作R()，即要素對應行值為 1 的所有要素。

的先行集合記作Q()，即要素對應列值為 1 的所有要素。

的共同集合記作T()，即R(i) ∩ Q()。

(1)UP型層級拓撲圖

UP 型層級圖，即結果優先的層級劃分，其抽取規則為：T() = R()。

只要可達集與共同集相同，就抽取出相關要素。每次抽取出來的要素放置在上方，依次按照由上往下的順序放置抽取出的要素。

(2)DOWN型層級拓撲圖

DOWN 型層級圖，即原因優先的層級劃分，其抽取規則為：T() = Q()。

每次抽取出來的要素放置在下方，依次按照由下往上的順序放置抽取出的要素。

UP 型和 DOWN 型屬於一組對立型的畫法，關係矩陣中的要素即為評價對象，評價對象之間的優劣（好壞，高低）通過有向線段表示，越優的評價對象置於最上層，因此最上層的評價對象即為帕累托最優，或者為最終結果。

算例

簡單偏序規則算例：

對於只有1列的決策矩陣，且該列為正向指標

以第三行第一列為例：其中A3到A1由於A1優於A3所以其值為真即為1

對於只有1列的決策矩陣，且該列為負向指標

優劣類的算例。

實際運用算例：

樣本均值屬於越小越好，為負向指標

標準誤差屬於越小越好，為負向指標。

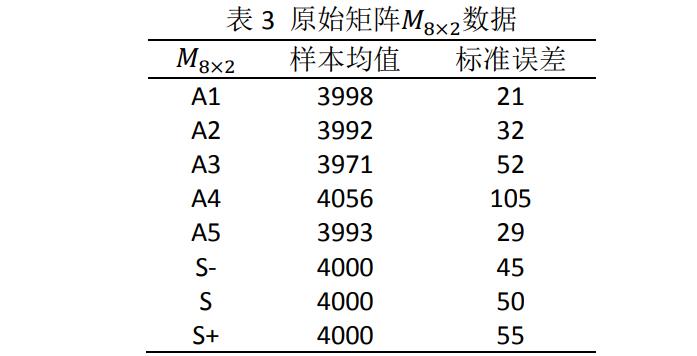
圖3 決策矩陣

關係矩陣為：

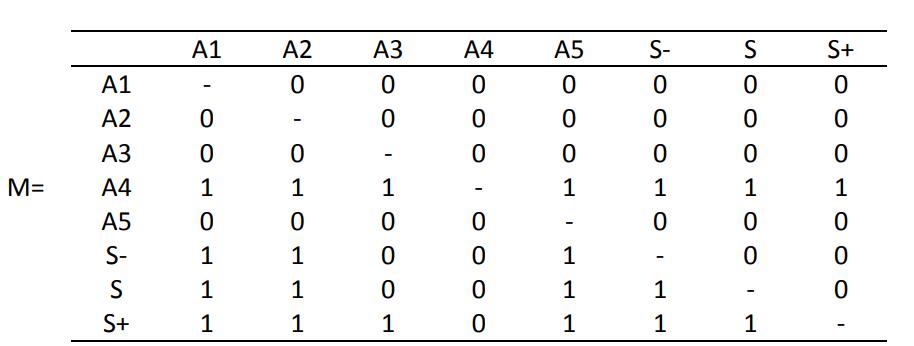
圖4 關係矩陣A亦為可達矩陣

以A4到A1為例即A1優於A4

最終的對抗層級拓撲圖5如下

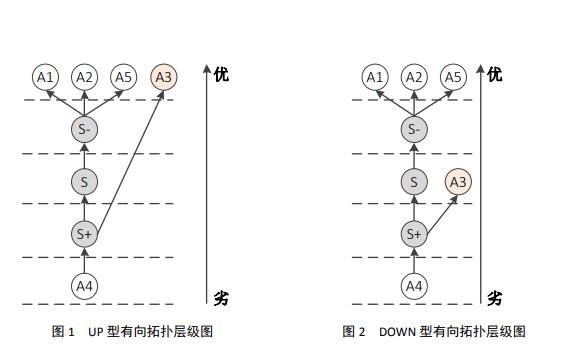
圖5 一組對抗的有向拓撲層級圖