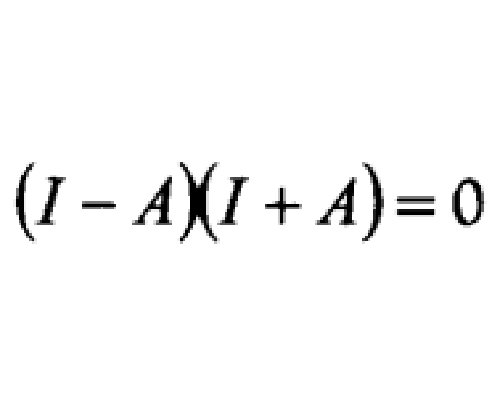對合矩陣

設A為n階方陣，I為n階單位陣，則滿足A²=I的方陣A稱為對合矩陣。滿足A²=A的方陣A稱為冪等矩陣。對於冪等矩陣和對合矩陣，有如下定理：(1)A為對合矩陣的充分必要條件是(I-A )(I+A)=0；(2)若A、B都是對合矩陣，則AB為對合矩陣的充分必要條件是AB=BA；(3)若A、B都是冪等矩陣，則A+B為冪等矩陣的充分必要條件是AB=-BA。

基本介紹

• 中文名：對合矩陣
• 外文名：involutory matrix
• 所屬學科：數學（矩陣）
• 充要條件：(I-A )(I+A)=0
• 相關概念：對角矩陣，單位矩陣，方陣等

定義

矩陣稱為對合矩陣(involutory matrix)，如果

其中為單位矩陣。

若是n階方陣，那么是對合矩陣的充分必要條件是是冪等矩陣；對合矩陣一定相似於對角陣

其中；若是對合矩陣，那么必有

相關定理

定理1 設是對合矩陣，則

(1)當n=2時，A形如

或者

或.

(2)是等冪矩陣。

定義 稱為共軛對合矩陣(coninvolutory matrix)或圓矩陣(circular matrix)，如果

定理2為共軛對合矩陣的充分必要條件是存在，使得

定理3設，下列條件等價：

(1) ，即E是共軛對合矩陣；

(2)；

(3) 是共軛對合矩陣。

定理4 設是非奇異矩陣，則

(1)存在共軛對合矩陣和非奇異矩陣，使得

而且E是的多項式。

(2)如果，其中滿足，是非奇異矩陣，那么

而且，若R和E可交換，則A和可交換(即是實的)；反之，若A和可交換，E是的多項式，則R和E可交換。

定理5 設，存在和共軛對合矩陣使得

的充分必要條件是非奇異矩陣使得