基本介紹
- 中文名：密碼學安全偽隨機數生成器
- 外文名：Cryptographically secure pseudorandom number generator
- 別稱：密碼學偽隨機數生成器
- 屬性：偽隨機數生成器
- 學科：密碼學
- 領域：密碼學
介紹,隨機性,統計學偽隨機性,密碼學安全偽隨機性,真隨機性,開放問題,相關條目,
介紹
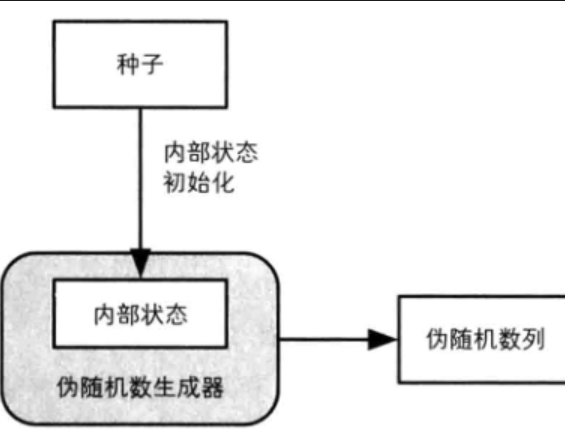
密碼學安全偽隨機數生成器（亦作密碼學偽隨機數生成器，英文：Cryptographically secure pseudorandom number generator，通稱CSPRNG），是一種能夠通過運算得出密碼學安全偽隨機數的偽隨機數生成器。相較於統計學偽隨機數生成器和更弱的偽隨機數生成器，CSPRNG所生成的密碼學安全偽隨機數具有額外的偽隨機屬性。
CSPRNG常被作為密碼學原件，用以搭建更複雜的密碼學套用。如，可變長CSPRNG和XOR函式搭配即構成流密碼的編解碼方法。
隨機性
密碼學領域的隨機性一般分為如下三類：
統計學偽隨機性
隨機比特序列匹配在統計學的隨機的定義。匹配該定義的比特序列的特點是，序列中“1”的數量約等於“0”的數量；同理，“01”、“00”、“10”、“11”的數量大致相同，以此類推。匹配該類別的隨機數生成方法的例子有線性同餘偽隨機數生成器。
密碼學安全偽隨機性
除了滿足統計學偽隨機性外，還需滿足“不能通過給定的隨機序列的一部分而以顯著大於1/2的機率在多項式時間內演算出比特序列的任何其他部分”。匹配該類別的密碼學安全偽隨機數生成器的例子如Trivium (算法)中的CSPRNG部分、SHA-2家族函式和計數器亦可被綁定以構建類似強度的CSPRNG。
可忽略函式
由可忽略速度增長的機率即為機率增長函式是可忽略函式。可忽略函式的定義如下：當輸入趨近於無窮大時，一個函式的增長速度小於任何多項式函式的反函式，則該函式是可忽略函式。換言之，
。比如說，我們知道，在輸入趨近於無窮大時，任何指數函式的增長速度大於任何多項式函式，因此，任何指數函式的反函式的增長速度一定小於任何多項式函式的反函式。指數函式的反函式是對數函式，因此，所有的對數函式都是可忽略函式。
真隨機性
除滿足以上兩點，還需要具備“不可重現性”。換言之，不能通過給定同樣的數據而多次演算出同一串比特序列。由於計算機算法均具備確定的特性，所以真隨機數無法由算法來生成。真隨機數的例子有放射性物質在某一時間點的衰變速度、某一地區的本底輻射值、正確使用設計良好的骰子所獲得的輸出等。
