基本介紹
- 中文名:完美圖
- 外文名:perfect graph
- 所屬學科:數學
- 所屬問題:組合學(圖與超圖)
- 簡介:一種特殊的簡單圖
基本介紹


















相關性質定理




































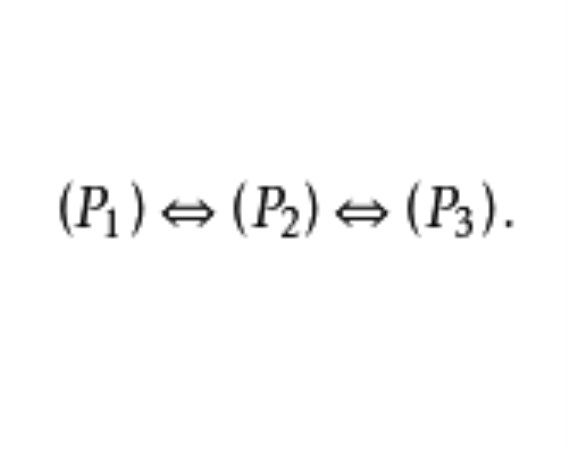






















































完美圖(perfect graph)是一種特殊的簡單圖,若圖G的任意一個節點導出圖H的色數χ(H)等於H的團數,則稱G是χ完美圖。若圖G的任意一個節點導出子圖H的獨立數α(H)等於H的團劃分數,則稱G是α完美圖,弱完美圖...
《完美圖庫·兒童美工資料全書:摺紙資料全書》中包含了兔子、恐龍、蝴蝶、花籃等100多種物品的摺紙方法,如果將它統統學會了,在套用基本的摺紙方法的基礎上,試著研發出屬於你自己的新的摺紙方法的話,你的創造力也會會噌噌地提高喔。即便...
《完美圖庫·動漫形象圖庫》是2018年湖北美術出版社出版的圖書,作者是李耀卿、馮馭,該書講述了大量性格鮮明、創意獨特的角色形象,在充滿想像力和創造力的卡通世界中,優秀而經典的動漫造型。編輯推薦 動漫造型設計發展至今,湧現了大量性格...
《完美圖集》是一款Android平台的套用。套用介紹 完美365圖集是分享唯美圖片、非主流圖片等圖片大全的美圖網,還有最新最全的汽車圖片、動漫圖片、風景圖片、搞笑圖片、美女圖片等圖片大全供你欣賞,是分享和收藏唯美圖片的最佳圖片網站。
《完美圖庫·兒童繪畫資料大參考(C)》由湖北美術出版社出版。《完美圖庫·兒童繪畫資料大參考(C)》是一部兒童繪畫的參考資料,其畫法介於正規繪畫和簡筆畫之間,涵蓋了動物、人物、植物、食物、建築、蔬果等圖例。目錄 動物篇 人物篇...
《完美圖庫·最全面的手繪pop實戰寶典·手繪pop廣告》2015年10月湖北美術出版社出版的圖書,作者是王猛,本書分為五章、十九節課程,課程包含基礎字型、變形字型、字型裝飾、創意字型、數字書寫、插圖繪製及套用、白底海報、彩底海報等。...
《完美圖庫:最精彩的兒童美術素材寶典(下)(黑白卷)》主要內容包括:卡通動物、卡通人物、神話人物、民族人物、古代人物、水滸人物、三國人物、西遊記人物、綜合場景、花卉植物、蔬菜瓜果、交通工具、生活用品。內容簡介 《完美圖庫:最精彩的...
《完美圖庫:最新鮮的環保製作精品寶典》是2013年湖北美術出版社出版的圖書,作者是王萍。內容簡介 《完美圖庫:最新鮮的環保製作精品寶典》是最時尚的卡通造型,最經典的美術素材,最實用的技法寶典。孩子們是天生喜歡圖畫的。視覺形象之於...
《完美圖庫:經典節慶手抄報黑板報設計大全》是2017年6月1日湖北美術出版社出版的圖書,作者是陳穎。內容簡介 《完美圖庫:經典節慶手抄報黑板報設計大全》是一本針對黑板報、手抄報設計的美術工具書。內容豐富,圖文並茂。《完美圖庫:...
《完美圖庫:經典節慶黑板報完全手冊》是2014年湖北美術出版社出版的圖書,作者是陳穎。內容簡介 在內容上力求與之不同,主要以知識性和常識性的文字資料為主,圍繞某一個主題,放射狀地介紹與之相關的小知識,並配以生動靚麗的版式圖,...
完美證件照,顧名思義就是完美的證件照。這種功能性人像攝影服務最早從新加坡傳入國內。完美證件照在拍攝之前,照相館一般都會根據顧客的相貌和氣質,化不同的妝、設計不同的髮型,而且還會準備一些服裝供顧客拍照時選用。完美證件照一般...
《完美圖形創新思維》是2018年9月30日蘇州大學出版社出版的圖書,作者是張開瑜。內容簡介 正方形(正四邊形)既是軸對稱圖形,又是中心對稱圖形,正方形集平行四邊形、矩形、菱形性質於一身,正方形是完美的正多邊形。正方形又是正...
《完美統計圖——Word/PPT/Excel數據可視化寶典》是2021年清華大學出版社出版的一本圖書,作者是鄧力、韓際平、潘璠。 內容簡介 統計圖是數據可視化的主角之一,本書講述如何製作規範的統計圖。全書共分4篇,用鮮活的實例,分別講述數...
《最好學的簡筆畫素材寶典-完美圖庫-下》是湖北美術出版社出版的圖書,作者是王萍 內容簡介 《完美圖庫:最好學的簡筆畫素材寶典(下)》由王萍編著。孩子們是天生喜歡圖畫的。視覺形象之於兒童,實在是一種教育,而所謂“陶冶”、“潛...
完美照片 《完美照片》是Joseph L. Scanlan執導的電影。電影信息 類型: 喜劇 製片國家/地區: 美國 上映日期: 1995-10-14 職員表 參考資料
《完美圖解胎教280天(全彩)》是2013年8月電子工業出版社出版的圖書,作者是吳光馳。內容簡介 本書根據不同的胎教內容劃分章節,在章節內以時間為順序,根據胎兒的發育情況向準媽媽講述如何對腹中的寶貝進行胎教,包括音樂胎教,運動、撫摸...
《完美圖解懷孕280天(全彩)》是2014年1月電子工業出版社出版的圖書,作者是吳光馳。內容簡介 本書在大結構上以內容為主線,而每一項內容當中再以時間為順序,全方位講述了懷孕280天需要關注的各方面內容,包括備孕、孕檢、孕期生活、...
《完美圖解懷孕每日一問》是2013年8月電子工業出版社出版的圖書,作者是吳光馳。內容簡介 本書由從事孕產育兒研究和臨床工作逾50年的首都兒研所專家吳光馳主任為孕媽媽精心編寫,內容包含孕期可能出現的各種問題及切實可行的解決方案,從...
《完美圖解物聯網IoT實操:使用JavaScript,Node.JS,Arduino,Raspberry Pi》是2017年8月電子工業出版社出版的書籍,作者是趙英傑。內容提要 《完美圖解物聯網技術》系列圖書是當前物聯網開發技術套用的集大成者。《完美圖解物聯網IoT實操...
《聰明人的一張紙工作整理術: 完美圖解》一書由高橋政史所著,2017年湖南文藝出版社出版發行。內容簡介 豐田汽車及P&G公司均貫徹一條原則,那便是“所有資料限於一張紙以內!”。這些大企業為什麼要堅持這么做呢? 因為這些企業認為,...
《完美圖解0~3歲寶寶安全餵養(全彩)》是2013年4月電子工業出版社出版的圖書,作者是吳光馳。內容簡介 本書根據不同年齡段寶寶對營養的特殊需求,詳細介紹餵養知識,並安排了相應的最科學的營養飲食方案,包括母乳、輔食、小菜譜、生病...
《完美旅圖·江西》是2017年中國地圖出版社出版的圖書,作者是中國地圖出版社。內容簡介 《“完美旅圖”系列 ·江西》是一張大幅面全彩印刷的特色實用旅遊地圖。圖正面為江西省旅遊交通圖和部分城市地圖以及資訊,地圖突出旅遊景點,搭配全面...
《完美旅圖·安徽旅遊地圖》是2017年中國地圖出版社出版的圖書,作者是中國地圖出版社。內容簡介 《“完美旅圖”系列·安徽》是一張大幅面全彩印刷的特色實用旅遊地圖。圖正面為安徽省旅遊交通圖和部分城市地圖以及資訊,地圖突出旅遊景點,...
《完美圖解懷孕280天》是2014年1月1日電子工業出版社出版的圖書,作者是吳光馳。內容簡介 本書是由從事孕產育兒研究和臨床工作逾50年的首都兒研所專家吳光馳主任為孕媽媽量身打造的,內容包含備孕、孕檢、孕期生活宜忌、胎教、孕期健康...
《完美的照片》是一款IOS平台的套用。是在iPhone應用程式 與她的溫柔、純潔的聲音,歌手,Shiho必然有魔法天賦交付。 在即興創作才華橫溢,天才吉他手,作為enthralls中島以聽眾與他的創造力。 由這兩個不可思議的成員,執行一個偉大的...
《完美旅圖·台灣旅遊地圖》是2017年中國圖書出版社出版的圖書,作者是中國圖書出版社。內容簡介 《“完美旅圖”系列 ·台灣》是一張大幅面全彩印刷的特色實用旅遊地圖。圖正面為台灣省旅遊交通圖和部分城市地圖以及資訊,地圖突出旅遊景點,...
《完美旅圖·福建》是2017年中國圖書出版社出版的圖書,作者是中國圖書出版社。內容簡介 《“完美旅圖”系列 ·福建》是一張大幅面全彩印刷的特色實用旅遊地圖。圖正面為福建省旅遊交通圖和部分城市地圖以及資訊,地圖突出旅遊景點,搭配全面...
