簡介
內容是這樣的:有一對雙生兄弟,一個登上一宇宙飛船作長程太空旅行,而另一個則留在地球。從相對地球靜止的參考繫上看,當旅行者回到地球後,我們發現他比他留在地球的兄弟更年輕。但是從相對飛船靜止的參考繫上看,我們發現他年紀更大。兩個互不相容的答案表示,唯一的可能是兩者年齡相同,似乎可以證偽洛倫茲變換。
這個佯謬的產生是基於對
狹義相對論中
時間膨脹的考慮。因為在各自的參考系中,兄弟倆都認為對方在運動。 而根據運動的時鐘變慢的原理, 似乎雙方都認為對方變年輕了。
佯謬產生的原因是
狹義相對論的時間膨脹原理僅僅對於
慣性參考系成立。 而旅行者要想返回, 必然至少有一次加速過程。 根據
廣義相對論,加速過程中的慣性力與引力等同, 而引力恰恰能夠導致
時間膨脹。(
廣義相對論可以解釋為什麼旅行者必然會有
時間膨脹,真正的計算並不是必須依賴廣義相對論。) 留守者處於(近似)慣性系所以留守者的計算是可靠的。所以最終的結果就是,旅行者會較之留守者年輕。
雙生子效應已經在1971年由科學家利用原子鐘繞地球一圈證實。 參看 Science 177 (4044): 166–168.
運動的鐘比靜止的鐘走得慢,相對論如是說。可鐘是什麼呢?它僅是那種做有規律的滴答聲的手錶呢,還是能把我們的定義擴大到把心臟的有規律跳動也包括進去的那種手錶呢?或者使人體內一個簡單的細胞也會延長其壽命的那種手錶呢?不會有任何限制阻止相對論適用於包括上列事物的任何過程。所有這些“鐘”即
自然界的一切變化過程在運動時都應慢下來。 讓我們帶著這種概念來探討一個有趣的可能性。讓我們假定有一對孿生子長到了20歲:哥哥叫高斯羅,是屬於不愛活動的那一類人;而他的妹妹,勃拉斯托,是個愛冒險的人。為了慶祝生日,她決定乘坐火箭到一個距離為20光年的遙遠星球去旅行。她以極接近於
光速的速度飛行,到達星球後立即動身回家。由於星球位於距離為20光年的遙遠之處,而且由於勃拉斯托幾乎是以光速飛行的,所以根據高斯羅在地球上的計算,這次旅行只用了40年稍多的時間。60歲的高斯羅匆忙地喝下一杯梅汁,急忙趕到火箭發射場去迎接他的妹妹。根據高斯羅的鐘,他的妹妹也應是60歲。但是,如果勃拉斯托生存在高速的環境中而且如果運動的鐘走得慢,那么導致衰老的身體發育過程就該放慢。那么我們就會預料到,一個年輕端莊的勃拉斯托從火箭上下來迎接她那年邁的孿生哥哥。
還有另外一個觀點,按照勃拉斯托對這次旅行的看法,她認為自始至終她都是處於靜止狀態,而高斯羅卻在地球上離開她飛走了,然後返回。她自己的照片表明,她已衰老了40歲,而且因為高斯羅是以高速運動的人,所以他的鐘應走得慢而正是他在他們重逢的時候應該年輕。
這兩種觀點看來都是正確的,都遵循
狹義相對論的定律,但顯然這兩種觀點不能都正確,佯謬就在此處,哪種觀點是正確的呢?為回答這一問題,我們必須指出,這次旅行並非像我們引導你去相信的那樣完全對稱。勃拉斯托為達到接近於
光速的速度必須經歷加速過程,然後經歷減速過程,而為了轉向回家的旅行再經歷加速過程。正是她經歷了加速過程,時間對她說來是遲延了。所以當這對雙生子重逢時,勃拉斯托確是年輕一些。這一真實情況已由一對電子鐘加以證實。一隻留下做為參照體,而另一隻鐘放在商業飛機上繞地球飛行,旅行後將兩隻鐘進行比較表明,旅行的那隻鐘“衰老”得少些。下面針對一種簡化形式簡略作一下解釋。
為使問題簡化,只討論這種情形,火箭經過極短時間加速到亞光速,飛行一段時間後,用極短時間調頭,又飛行一段時間,用極短時間減速與地球相遇。這樣處理的目的是略去加速和減速造成的影響。在地球參考系中很好討論,火箭始終是動鐘,重逢時高斯羅比勃拉斯托年輕。在火箭參考系內,地球在勻速過程中是動鐘,時間進程比火箭內慢,但最關鍵的地方是火箭掉頭的過程。在掉頭過程中,地球由火箭後方很遠的地方經過極短的時間划過半個圓周,到達火箭的前方很遠的地方。這是一個"超光速"過程。只是這種超光速與相對論並不矛盾,這種"超光速"並不能傳遞任何信息,不是真正意義上的超光速。如果沒有這個掉頭過程,火箭與地球就不能相遇,由於不同的參考系沒有統一的時間,因此無法比較他們的年齡,只有在他們相遇時才可以比較。火箭掉頭後,高斯羅不能直接接受勃拉斯托的信息,因為信息傳遞需要時間。高斯羅看到的實際過程是在掉頭過程中,地球的時間進度猛地加快了。在高斯羅看來,勃拉斯托先是比高斯羅年輕,接著在掉頭時迅速衰老,返航時,勃拉斯托又比自己衰老的慢了。重逢時,高斯羅仍比勃拉斯托年輕。也就是說,相對論不存在邏輯上的矛盾。
注意,這不是基於不同參照系的觀測效果,而是勃拉斯托和高斯羅各自度過的固有時間的差異。固有時間可以用各自在閔氏空間中運動軌跡的四維長度除以光速得到,這個四維長度是不依賴於參照系的。
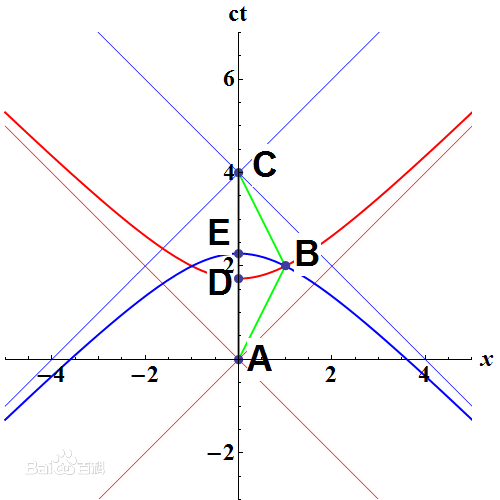
右面的只有一個空間軸x的時空圖可能對理解本題有些幫助,假定高斯羅出行到達的最遠點為L,出行去程速度和回程速度都是v;。則勃拉斯托的世界線是沿ADEC的一條直線,高斯羅的世界線是折線ABC。為了繪圖方便,圖中L取成1,v=0.5 c。
令β=v/c,則B點坐標為:x =L,ct=L/β;
C點坐標為: x =0,ct=2*L/β紅色的雙曲線的曲線方程為:
 雙生子的時空圖
雙生子的時空圖藍色雙曲線方程為:
由於閔可夫斯基時空的特點,四維線長可以用公式:
來計算。
因此連線A點到紅色的雙曲線上的任何一點的直線段的四維線長,都是相等的(對比歐氏空間,歐氏空間中和一點距離相當的點,是在一個圓周上。而閔氏時空則是在兩條雙曲線上)。也就是從A點開始沿直線段走到紅色雙曲線上任意一點所花費的固有時,也就是線長除以光速都相等。同樣的道理,藍色雙曲線上的點,沿直線段走到C點所花費的固有時也都相等。因此有AB的固有時等於AD的固有時,BC的固有時等於EC的固有時,而線段AC比AD加上EC還要長出DE一段,所以可以知道ADEC這條路徑比ABC這條路徑耗費的固有時要長。這樣留在地球上的弟弟要比出行的哥哥度過了更長的時間,也就是說,見面時高斯羅比妹妹年輕。
選用不同的慣性系作為基準坐標系,A、B、C、D、E點,會沿雙曲線移動,因此固有時不變,也就是說在任何參照系看,結果都是一樣的。接下來的幾幅時空圖展現了特點。左邊的圖是把高斯羅去程的慣性系作為基準坐標系,右邊是把高斯羅回程的慣性系作為基準坐標系。左圖中AB和右圖中BC為垂直線,說明高斯羅相對基準坐標系來說是靜止的。
這兩個圖中,ADEC依然比ABC長出DE那段長度。圖中這條雙曲線與其對稱軸的交點,只是在基準坐標系中看起來有點特殊,事實上,雙曲線上的任一點,都可以找到一個基準坐標系,使得它成為這條雙曲線與其對稱軸的交點。因此雙曲線上的點都是平權的。類似的,在最初的那幅時空圖中,D、E分別是紅色雙曲線和藍色雙曲線與其對稱軸的交點,而在左圖中B成了紅色雙曲線與其對稱軸的交點,在右圖中,B成了藍色雙曲線與其對稱軸的交點。
 雙生子的時空圖
雙生子的時空圖
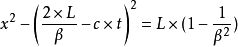

 雙生子的時空圖
雙生子的時空圖