多項式長除法

多項式長除法是代數中的一種算法，用一個同次或低次的多項式去除另一個多項式。是常見算數技巧長除法的一個推廣版本。它可以很容易地手算，因為它將一個相對複雜的除法問題分解成更小的一些問題。

值得注意的是，多項式除以多項式，如果採用連等式的形式化簡，類似於分式的約分，即：先將被除式與除式分別因式分解，然後消掉二者都有的公因式，得出最後的結果。對於次數較高的多項式進行因式分解，往往需要大量的添項、拆項等技巧，並且線索有時極其不明顯，如果用連等式進行化簡的話，則運算效率遠遠不及長除法。這也是現行國中數學教材不涉及對多項式除以多項式進行化簡的原因之一。

基本介紹

• 中文名：多項式長除法
• 外文名：polynomial long division
• 學科：數學，多項式代數

計算方法

計算

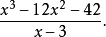
把被除式、除式按某個字母作降冪排列，缺項補零，寫成以下形式：

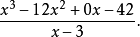
然後商和餘數可以這樣計算：

1. 用分子的第一項除以分母的最高次項（即次數最高的項，此處為x），得到首商，寫在橫線之上（x³÷x=x²）。
   
2. 將分母乘以首商，乘積寫在分子前兩項之下（同類項對齊） x²×(x−3) =x³−3x²
   
3. 從分子的相應項中減去剛得到的乘積（消去相等項，把不相等的項結合起來），得到第一餘式，寫在下面。然後，將分子的下一項“拿下來”。
   
4. 把第一餘式當作新的被除式，重複前三步，得到次商與第二餘式（直到餘式為零或餘式的次數低於除式的次數時為止．被除式=除式×商式+餘式 ）
   

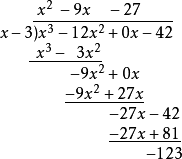
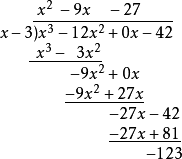
5. 重複第四步，得到三商與第三餘式。餘式小於除式次數，運算結束。

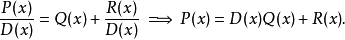
橫線之上的多項式即為商，而剩下的 (-123) 就是餘數。

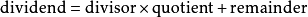
算數的長除法可以看做以上算法的一個特殊情形，即所有x被替換為10的情形。

除法變換

使用多項式長除法可以將一個多項式寫成 除數-商 的形式（經常很有用）。 考慮多項式P(x),D(x) （(D)的次數 < (P)的次數）。 然後，對某個商多項式Q(x) 和餘數多項式R(x) （(R)的係數 < (D)的係數），

這種變換叫做除法變換，是從算術等式

得到的。