多面體的運算(operations of polytopes)是多面體間的變換,即由兩個多面體對應出一個新多面體的映射。
基本介紹
- 中文名:多面體運算
- 外文名:operations of polytopes
- 所屬學科:數學
- 所屬問題:組合學(組合多面形)
- 簡介:多面體間的變換
多面體之和

多面體之積

多面體之極



多面體投影像





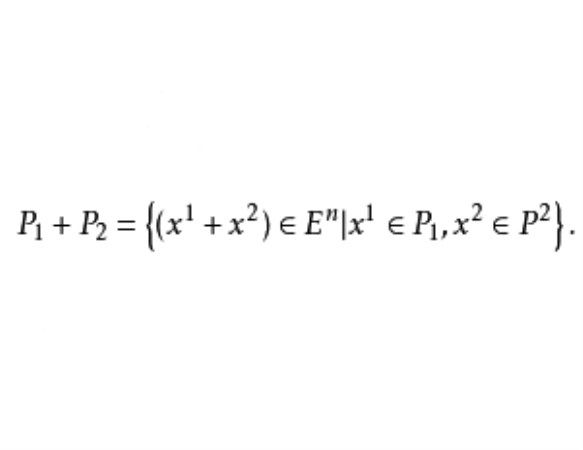
多面體的運算(operations of polytopes)是多面體間的變換,即由兩個多面體對應出一個新多面體的映射。










多面體的運算(operations of polytopes)是多面體間的變換,即由兩個多面體對應出一個新多面體的映射。多面體之和多面體之和(sum of polytopes)是多面體P1和P2之和,記為多面形的分解定理...
多面體之和是一類多面體運算,多面體P₁和P₂之和,記為 多面形的分解定理使用的正是此類運算。相鄰多面體的和是相鄰多面體的一種合成,即由相鄰多面體導出的一個多面體,兩個相鄰多面體,剔除其所有的公共點後,所形成的第三個多面體,稱為兩個相鄰多面體的和。相關介紹 當凸多面形為滿足線性不等式組 的...
康威多面體表示法是用來描述多面體的一種方法。 一般是用種子多面體(seed)為基礎並標示對種子多面體做的操作或運算。種子多面體一般都為正多面體或正多邊形密鋪,表示的字母則取他們名字的第一個字母,例如:T = 正四面體 (Tetrahedron)C = 正方體 (Cube)O = 正八面體 (Octahedron)D = 正十二面體 (Dodecahedron...
《多面體編譯理論與深度學習實踐》是2022年清華大學出版社出版的圖書,作者是趙捷、李寶亮。內容簡介 本書分十大章節和三章附錄章節,以現代體系結構特徵為目標,從理論、方法及套用等不同角度,詳細描述了各種提升程式並行性、數據局部性及適配目標架構特徵的高級編譯最佳化技術。本書還結合深度學習套用場景展開討論,介紹了...
在歐拉公式中, f (p)=V+F-E 叫作歐拉示性數。歐拉定理告訴人們,簡單多面體f (p)=2。除簡單多面體外,還有非簡單多面體。例如,將長方體挖去一個洞,連結底面相應頂點得到的多面體。它的表面不能經過連續變形變為一個球面,而能變為一個環面。其歐拉示性數f (p)=16+16-32=0,即帶一個洞的多面體的...
第1天多面體與旋轉體 【題型一】多面體相關計算 【題型二】旋轉體相關計算 第2天球 【題型一】半徑、面積、體積等計算 【題型二】多面體外接球問題 第3天平行垂直的判斷與證明 【題型一】平行的判斷與證明 【題型二】垂直的判斷與證明 第4天角度距離計算(上)——幾何法 【題型一】線線角 【題型二】線面角 ...
這個公式叫做歐拉公式.它表明2這個數是簡單多面體表面在連續變形下不變的數。分式 當r=0或1時式子的值為0,當r=2時值為1,當r=3時值為a+b+c。平面幾何 設△ABC的外心為O,內心為I,外接圓半徑為R,內切圓半徑為r,又記外心、內心的距離OI為d,則有 (1)式稱為歐拉公式。為了證明(1)式,我們現...
在數學中,橫截相交是描述空間如何相交的概念,並在一般的立場上發揮作用。 它形成了差分拓撲中通用交集法。 通過考慮交點處的交叉空間的線性化來定義。定義 給定有限維平滑多面體的兩個子流形橫截相交,它們在每個相交點處產生多面體的切線空間。不相交的多面體是橫截的。如果多面體具有互補尺寸(即它們的尺寸加在...
在定理的正確敘述中,多面體的上同調系統的一族同態還應與周學光建立的第二上同調運算ψi可交換。周學光關於糾正Shiraiwa定理的一系列論文的發表,在國際拓撲界引起廣泛而強烈的反響。著名代數拓撲學家J.F.亞當斯(Adams)在美國《數學評論》中用大量篇幅介紹周學光的工作。亞當斯在評論中認為所舉的反例是正確的,但是...
計算幾何算法庫(CGAL),提供計算幾何相關的數據結構和算法,諸如三角剖分(2D約束三角剖分及二維和三維Delaunay三角剖分),Voronoi圖(二維和三維的點,2D加權Voronoi圖,分割Voronoi圖等),多邊形(布爾操作,偏置),多面體(布爾運算),曲線整理及其套用,格線生成(二維Delaunay格線生成和三維表面和體積格線生成等...
流這個概念是由德拉姆(deRham,G. W. )為研究霍奇理論而引入的,由於一個曲面決定於對於定義在它上面的任意m階光滑微分形式的積分運算,因此m維幾何曲面可以分析地表示成一個流。特別地,由點 生成的單純形若落在U內,則它也代表-一個流。這種流的整係數線性組合稱為U中的一一個整係數多面體鏈。推廣 利用邊緣...
在緊多面體的情況,這兩種同調群都同構於按單純剖分得到的同調群。在以某種環為係數的上同調群中可以引入乘法使之成為上同調環。為了更好地利用上同調群,在其上引入了所謂上同調運算的額外結構,例如斯廷羅德冪,龐特里亞金冪等等。由斯廷羅德冪發展成為斯廷羅德代數的研究,大大豐富了同調論的內容。
幾何組合與凸和離散幾何有關,特別是多面體組合。例如,它詢問多少個凸多面體可以具有多少個面。多面體的度量性質也起著重要的作用,例如關於凸多面體剛度的Cauchy定理。也考慮特殊的多面體,如permutohedra,associahedra和Birkhoff多形體。我們應該注意到組合幾何對於離散幾何來說是一個老式的名字。拓撲組合 概念和拓撲方法...
如今幾乎每一個數學領域都可以看到歐拉的名字,從初等幾何的歐拉線、多面體的歐拉定理、立體解析幾何的歐拉變換公式、四次方程的歐拉解法,到數論中的歐拉函式、微分方程的歐拉方程、級數論的歐拉常數、變分學的歐拉方程、複變函數的歐拉公式等等。他對數學分析的貢獻更獨具匠心,《無窮小分析引論》一書便是他劃時代的...
