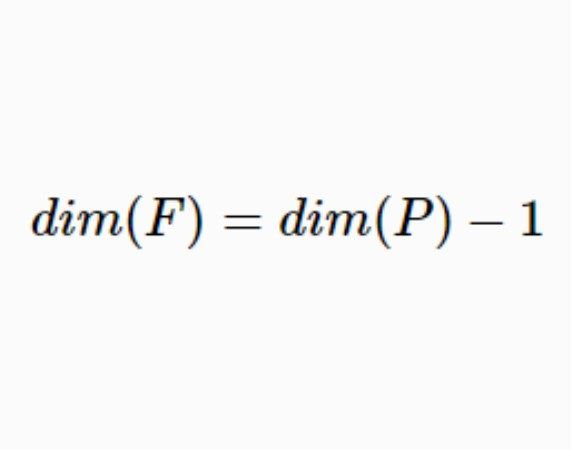多面體半擬陣

多面體半擬陣(semi-matroid of polytope)是與多面體關聯的一類組合構形，當兩個簡單多面體的半擬陣同構時，它們對應的多面體是組合等價的；而且，反之亦然。

基本介紹

• 中文名：多面體半擬陣
• 外文名：semi-matroid of polytope
• 所屬學科：數學
• 所屬問題：組合學（組合多面形)

基本介紹

多面體半擬陣是一個簡單多面體M關聯的半擬陣，F為M的所有極大面構成的集族，V為M的頂點集。M為簡單多面體是指M的每一個頂點均正好關聯d個極大面，d為M的維數，二元組滿足下述半擬陣條件：

1.V的每個頂點v正好關聯d個極大面，或者說，v正好包含在d個極大面之中。

2.已知任一個由個極大面構成的子集，或者存在兩個頂點，使得這極大面都與這兩個頂點關聯，或者不存在這樣的頂點。

當兩個簡單多面體的半擬陣同構時，它們對應的多面體是組合等價的；而且，反之亦然。

相關概念

極大面

定義 若多面體P的面F滿足，則稱F為P的一個極大面(facet)。

命題 若F是多面體的一個極大面，是多面體P的不等式指標集，則存在某個指標，使得不等式為極大面F的表示，即

簡單多面體

若多面體符合條件：①一切面都是簡單多邊形；②各棱之間、棱與面的內部都沒有公共點；③頂點不附著於各面的內部或各棱之上；④共有一個頂點的一切面角，圍拱著這個頂點構成一個多面角，則這樣的多面體叫做簡單多面體。

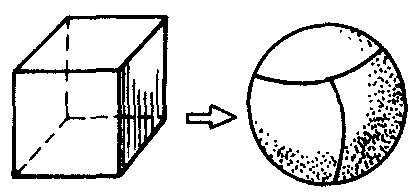
圖1 簡單多面體

簡單多面體也可以這樣理解：我們構想一個多面體的面是用橡膠簿膜做成的，若充以氣體，則它就會連續(不破裂)變形.表面連續變形，可變形為球面的多面體叫做簡單多面體.否則為非簡單多面體.如圖1中的正方體表面連續變形後可以變成球面，所以正方體是簡單多面體.而圖2中的多面體(正方體中間挖去一個方孔)表面連續變形後，將變成一個環面，而不是一個球面，因此這個多面體不是簡單多面體.

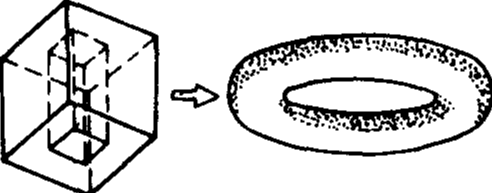
圖2 多面體

稜柱、稜錐、稜台、正多面體、凸多面體都是簡單多面體。