模型介紹 如果一個模型包含了不同層次的測量變數,稱為多層次模型 (multilevel model)。在多層次模型中,各脈絡可估計出一條低層次的個別直線方程式。在這條回歸線中,通常各脈絡都有相同的解釋變數(explanatory variables)(解釋變數即為自變數(independent variable),在回歸分析中又稱為預測變數(predictor or predictive variable))與結果(out.come)(結果即為因變數(dependent variable),後也以反應變數(response variable)稱呼之,有時則稱為結果變數(outcome variable)),但是有不同的回歸係數。這些個別回歸方程式被一個高層次模型所聯結,在高層次模型中,第一層次的回歸係數可被第二層次的解釋變數所解釋。
用來聯結這些個別回歸方程式的高階模型的特性,決定了整個模型對於數據分析的方式。在實務上有多種處理方式,最開始的起點是沒有高層模式來整合個別方程式的模式,此時每一個脈絡各擁有一個回歸方程式。雖然這是很自然應該為之的做法,但是從統計的觀點來看,此一做法並沒有任何新意。
進一步講,將第一階層各脈絡的回歸係數作為第二階層的反應變數(response variable),稱為“斜率結果(slope-as-outcome)”分析(Burstein,et a1. 1978)。從統計的觀點來看,在各組內與各組間所進行的回歸分析彼此並無關聯,他們仍是個別進行的分析。不論是未經聯結或已被高層模式聯結的分析,回歸係數都是固定數值(fixed),麗非隨機變動(random)。如果一個模型利用了全部數據進行分析,則被稱為變動係數模型(varying coefficient model),此種模型的分析方法即如其名,是把每一個組分開進行估計,因此每一組擁有各自的一組回歸係數。
每一個組進行個別回歸分析之後,再以離層解釋變數來解釋第一層係數的這種說法,尚不足以說明多層次模型的內涵。基本上,多層次模型的基本特性是將研究者所關心的特定層次的數據,用不同的模型通過統計的整合來加以分折。
最簡單的整合模型是隨機係數模型(random coefficient model)。這種模型中,第一層的回歸係數在第二層被以隨機變數來處理,這意味著第一層回歸係數是從某個機率分配取樣而得,此一分配最重要的參數——平均數與方差,可從多層次模型中估計得出的參數所獲得。一般來說,在隨機係數模型中加入第二階層的解釋變數是一般通則性的做法,也是非常有用的策略,因此一般被通稱為多層次模型。
使用原因 在考慮社會與健康科學所關注的幾乎所有現象時,我們都應該注重事件情境的重要性。例如,社會環境的緊張可能影響個體的情緒;藥物對心理狀態的改善受使用者所處社會結構的影響;早期童年發展與一系列環境條件相關,如飲食習慣、環境刺激、環境污染、與母親的關係等;青少年危險行為和他們所處的成人世界的結構化行為有關係;孩子的教育成果會被課堂、學校以及教學體制所制約。以上都是個體行為受到社會環境影響的例子。實際上,情境的作用遠不止這些。例如,婚姻關係中離婚的選擇與宗教和文化背景顯著相關;組織氛圍影響群體選擇;醫療機構利潤受衛生維護組織(HMO)返款政策的強烈影響。上述所有例子的共同點在於,某一個高層次特徵的存在或其發生過程影響著低層次特徵的存在或發生。由於概念是建構於不同層次的,因此概念間的關係也發生在多層次之間,從而需要特殊的分析工具才能加以估計。這就是多層次模型的主題。
儘管情境如此重要,但那些並不能解決多層次數據與理論問題的分析工具卻常被運用於健康與社會科學研究中。在研究發展的早期階段,這是由於多層次分析工具的缺失造成的。然而在多層次模型已經相當完善的今天,研究者卻繼續使用著簡單化的單一層次模型。
社會科學中某些傳統的認識論或許可以解釋這種現象。首先是實證主義研究傳統的廣泛影響,即便是在多年以前,科學哲學已經認識到實證主義並不足以建立生物、健康以及社會科學的研究架構,我們卻傾向於追隨實證主義傳統來進行研究設計和分析。例如在研究中,我們會控制實驗條件、使用控制組和對照組以及在模型中控制協變數的影響以提供更準確的統計推論,但在測量和估計超個體層面的環境性因素時,我們卻面臨非常嚴重的局限。
實證主義在處理科學問題時最為有效,因其面對的大多是封閉體系中的問題。這類封閉體系中的行為常常可以用少數幾個變數來預測,比如行星的位移可用其質量和速度來估計。健康與社會科學處理的是更為複雜的開放體系中的問題,其中外部環境因素常常無法被控制、限定或去除,從而使能夠測量和分析環境因素的多層次模型顯得尤為重要。讓我們來看一個醫學模型的例子。它以簡化的視角來看待健康,將疾病視為可被藥物刺激而修正的一種身體缺陷,但現代流行病學則試圖確定疾病的風險因素。以心血管疾病為例,現代流行病學通過一系列有力的研究設計(如控制組研究) 和分析工具( 如對相對患病風險的logistic 回歸)來確定重要的患病風險因素,包括基因體質、身體狀況( 高血壓)、行為習慣(吸菸、運動)、文化背景(種族)和環境(醫療條件)。然而,雖然這些因素明顯作用於不同層面,但它們卻總是於個體層面被測量(比如通過調查),並且各個不同層面的因素髮生作用的機制也很少被關注。比如,缺乏運動是個體選擇造成的,還是由於社區生態導致個體在社區內缺乏運動條件造成的?
儘管如此,在行為、健康和社會科學中,多層次模型卻正在獲得越來越多的關注和使用。在美國國立衛生研究院2000 年的報告《走向多層次分析:健康研究中社會和文化維度的進步與前景》(行為及社會科學研究辦公室,2000)中,這份關於新議題的報告提出了兩個研究目標:一是擴展與健康相關的社會科學研究;二是將社會科學研究整合進跨學科的、多層次的健康研究中。為了實現這兩個目標,報告提出了以下建議:
支持發展高質量的社會科學方法。這方面的挑戰 包括:群體、網路、鄰里、社區層次的測量;縱向數據研究 方法的發展;整合不同量化與質化研究的多層次研究設 計以及數據蒐集和分析方法的改進。
表1 健康研究的不同層次:以菸草控制為例 分析層次
示例:菸草控制研究
文化/政治
測量菸草稅對人口吸菸比例的影響
社會/環境
測量家庭與同輩影響在青少年吸菸行為中的相對重要性
行為/心理
設計有效的吸菸預防與禁止項目
器官
防止吸菸者體內腫瘤的形成
細胞
尼古丁攝人的新陳代謝研究
分子/基因
尼古丁依賴的基因研究
表1以菸草控制為例,這份報告展示了各個分析層次之間的相互影響,並以此構建概念框架。菸草控制研究關注從基因到社會文化、政治的各個層面。儘管可以將研究局限於任何一個層面,但大多數重要的研究會關注各個層面之間的聯繫。例如,在了解各種基因的尼古丁依賴的基礎上,我們可以對各基因類型進行恰當的預防性干預。
2003年美國國家科學院醫學研究所關於公眾健康的報告更清楚地反映了多層次因素的相互依賴性和層級化特徵。圖1展現了健康決定因素的社會生態模型。該報告強調,公共健康專家以及研究者必須理解和套用社會生態學路徑,以期成功地改善國家整體的健康狀況。
圖1影響健康的決定因素的多層次索引圖 理論依據 簡單地說,由於大多數研究對象在本質上是多層次的,因而我們應使用多層次的理論和分析工具,否則我們將面臨嚴重的問題。
例如,在集體層面蒐集和分析健康行為數據是非常普遍的。流行病學顯示,在那些居民日常食譜中脂肪含量較高的
國家,其乳腺癌致死的比例也較高(Carroll,1975)。如此看來,攝人更多脂肪的女性更易患乳腺癌似乎是一個合理的推論。然而這一推論卻是一個生態學謬誤,其中,群體間的關係被假設同樣存在於個體之間(Freedman,1999)。事實上,近期的健康研究表明,在個體層面,脂肪攝人量與乳腺癌之間的關係並不明顯(Holmes et al.,1999)。
這類謬誤也可能以另一種方式出現。在行為科學中,數據常常從個體處蒐集,然後集合成為群體數據以說明個體所從屬的群體信息,這可能導致原子謬誤,即群體信息被不正確地從個體信息中推論出來( Hox,2002)。儘管從個體層面獲取整個生態的特徵信息並非不可能,如MOOS 關於社會氣候的推論就是一個成功的例子(Moos,1996),然而Shinn 和Rapkin卻令人信服地指出,這類推論並不可靠,更可取的方法是使用群體層次的測量和分析工具來獲取群體信息。我們有必要考慮集群和成員在屬性上的社會學區別(Lazarsfeld & Menzel,1969)。成員從屬於集群,但集群與其成員的多種屬性(變數)卻可能同時被測量和分析。Lazsarfeld 和Menzel 定義了集群的分析屬性、結構屬性以及整體屬性。分析屬性通過集合集群內的個體信息來獲得(例如,一個城市中西班牙裔人口的比例),結構屬性建立在集群成員之間的關係上,而整體屬性則是集群本身的特徵,並不受個體成員的影響(O'Brien,2000)。例如,學校的禁菸政策就是學校這一集群的整體屬性。從這一框架可以看出,以上的謬誤存在於推論而非測量中。我們完全可以從低維度的成員信息中獲得高層次的集群特徵。當某一特定層面的關係被不恰當地假定於其他層面時,上述謬誤就出現了。
統計依據 當面對這些複雜的概念問題時,即使所處理的數據與假設實為多個層次的,社會科學研究者仍傾向於使用傳統的個體層次模型來解決問題。若分解群體層次的信息至個體層面,從而將多元回歸中的變數限定在個體分析單位中,則至少會導致兩方面的問題:首先,所有未被擬合入模型的背景信息最終都被包含在模型的個體層次誤差項中(Duncan,Jones &Moon,1998 ),而由於相同背景下的個體層次誤差項必然相關,則違反了多元回歸的基本假設;其次,忽略背景因素則意味著各回歸係數同等作用於一切情境,這實則反映了“在不同背景條件下,事物的發生機制本質相同”的錯誤觀點(Duncan etal.,1998:98)。
通過引入個體分組情況的影響,
方差 分析(ANOVA) 與
協方差 分析(ANCOVA)可以部分地解決這些統計問題,但缺陷仍然存在:首先,當個體的組別較多時,這類模型必然使用較多的參數而大大降低解釋力和簡約性;其次,這些組別參數往往被作為固定效應引人,從而忽略了群組層面的隨機變數;最後,在處理缺失數據或不均衡設計時,方差分析不夠靈活。
表2 健康和社會科學研究中的多層次模型與結構 多層次模型
多層次結構
示例
物理
個體存在於物理環境之中,這包括生物環境、生態環境以及物理建構環境
Diez-Roux等人(2001)Perkins 等人(1993)
社會
個體存在於社會結構之中,包括家庭、同輩以及其他社會網路
Buka等人(2003)Rice 等人(1998)
組織
個體和小群體存在於特定的組織之中,重要的組織特徵包括規模、管理結構、群體交流、組織目標等
Maes 與Lievens(2003)
政治/文化
個體或群體存在於特定的社會政治環境、文化環境和歷史環境中
Lochner等人(2001)
時間
對某一個體在不同時點的多次觀察
Boyle 與Willms(2001)
分析
個體研究中的多元效應測量(如元研究)
Goldstein 等人(2000)Raudenbush 與Bryk(1985)
技術知識 上述討論的主要目的在於對社會與健康科學研究中的多層次模型統計方法做相對非技術性的介紹。多層次模型的技術性內容主要有二層模型及其擬合方法,包括數據準備、模型估計、模型解釋、假設檢驗、模型假設條件檢驗以及中心化。其次還有對多層次模型的擴展套用,包括對非連續型因變數和非常態分配型因變數的處理以及使用多層次方法分析縱向數據和構建三層模型。這些內容都有其與
多元回歸 的相似性。
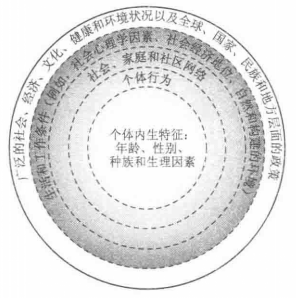 圖1影響健康的決定因素的多層次索引圖
圖1影響健康的決定因素的多層次索引圖
