塹堵是算學術語。是一長方體沿不在同一面上的相對兩棱斜解所得的立體，即兩底面為直角三角形的三稜柱。其體積公式為：V=abh/2，(其中a，b，h分別是塹堵底面長、寬及高)。
基本介紹
- 中文名：塹堵
- 拼音：qiàn dǔ
- 所屬學科：數學
- 簡介：兩底面為直角三角形的三稜柱
- 體積公式：V=abh/2
- 相關人物：劉徽、梅文鼎
基本介紹,史書記載,劉徽的證明,
基本介紹
塹堵是一個長方體沿不在同一面上的相對兩棱斜解所得的立體，即兩底面為直角三角形的三稜柱。最早的文字記載見於《九章算術》“商功”章。《九章算術·商功》劉徽註：“邪解立方得二塹堵，邪解塹堵，其一為陽馬，其一為鱉臑。”鱉臑系一四面體，其三面皆為勾股形，梅文鼎稱為立三角形。立三角形以其一面為底，其他三面聚於一點為頂點，在頂點旁三側面的頂角和三側面間的三個二面角與球面三角形的三弧三角相當。《九章算術》給出其體積公式
，其中
為底面兩直角邊，h為高。若
則成為三品棋之一。
圖1
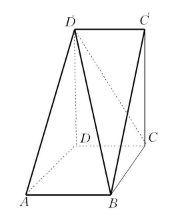圖2史書記載
塹堵是沿長方體相對兩棱斜解所得的楔形體，下面二段分別是其體積公式：，(其中a，b，h分別是塹堵底面長、寬及高)及劉徽的證明。
①術曰：廣袤相乘，以高乘之，二而一。（漢《九章算術·商功》）
②邪解立方得兩塹堵。雖復隨方*，亦為塹堵，故二而一。此則合所規棋(原本作“冪”，錢寶琮校)，推其物體，蓋為塹上疊也。其形如城，而無上廣，與所規棋形異而同實。（《九章算術·商功》三國魏·劉徽注）
[注]* 隨，音義通橢，橢方即長方體。
劉徽的證明
劉徽原理
為了推證除直線型柱體以外其它直線型立體的體積，在前人的基礎上，劉徽提出三種基本幾何體，即“塹堵”、“陽馬”、“鱉鱉臑 ”。“塹堵”即是底為直角三角形的直稜柱，如商功章第14問劉徽注稱：“邪解立方得兩塹堵。雖復橢方，亦為塹堵”。“陽馬”即是底為正方形或長方形一側棱與底垂直的四稜錐，如商功章第15問劉徽注稱：“陽馬之形，方錐一隅也。今謂四柱屋隅為陽馬”。“鱉臑”即是側面都是直角三角形的四面體，如商功章第15問劉
徽注稱：“邪解立方得兩塹堵。邪解塹堵，其一為陽馬，一為鱉臑”。(如圖3、圖4、圖5)。
劉徽為了推證直線型立體的體積算法，於是提出三種基本幾何體，其中“塹堵”體積算法為其三度乘積的二分之一，如劉徽注說：“邪解立方得兩塹堵。雖復橢方，亦為塹堵，故二而一”。即
塹堵體積=1/2(長×寬×高)，
但是，為了推求陽馬、鱉臑的體積算法，劉徽提出“陽馬居二，鱉臑居一，不易之率也”。這一提法，稱之為“劉徽原理”。劉徽還說：“邪解立方得兩塹堵。邪解塹堵，其一為陽馬，一為鱉臑”。可見，劉徽深知三度分別相等之陽馬與鱉臑體積相加之和為一塹堵體積；而陽馬與鱉臑體積之比為二比一。即
陽馬體積+鱉臑體積=塹堵體積；
陽馬體積：鱉臑體積=2：1。
前一問題，即陽馬與鱉臑體積之和為塹堵體積，是十分明顯的。如果能證明後一問題的正確性，即證明了陽馬與鱉臑體積之比為二比一，也即證明“劉徽原理”的正確性；則不難推出陽馬、鱉臑的體積算法。據此，劉徽注說：
“使鱉臑廣、袤、高各二尺，用塹堵、鱉臑之綦各二，皆用赤綦。又使陽馬之廣、袤、高各二尺。用立方之綦一，塹堵、陽馬之綦各二，皆用黑綦。綦之赤、黑，接為塹堵，廣、袤、高各二尺。於是中效其廣、袤，又中分其高，令赤、黑塹堵各自適當一方，高一尺方一尺，每二分鱉臑則一陽馬也。其餘兩端，各積本體，合成一方焉。是為別種而方者率居三，通其體而方者率居一。雖方隨綦改，而固有常然之勢也。按餘數具而可知者有一、二之別，即一、二之率定矣。其於理也豈虛矣。若為數而窮之，置余廣、袤、高之數各半之，則四分之2-Y,．可知也。半之彌少，其餘彌細。至細日微，微則無形。由是言之，安取余哉。數而求窮之者，謂以情推，不用籌算”。
劉徽按上面所述，利用極限觀念證明了“劉徽原理”。即是取兩個赤色塹堵模型，兩個赤色鱉臑模型，使拼接成一個廣、袤、高各二尺的赤鱉臑；再取一個黑色立方模型，兩個黑色塹堵模型，兩個黑色陽馬模型，使拼接成一個廣、袤、高各二尺的黑陽馬；然後將赤鱉臑與黑陽馬相合拼接成一個廣、袤、高各二尺的“赤黑塹堵”。中分此“赤黑塹堵”的廣、袤、高，則得小黑塹堵二，小赤塹堵二，小黑立方一，和小赤鱉臑二，小黑陽馬二；再將兩個小黑塹堵拼接成小黑立方一，將兩個小赤塹堵拼接成小赤立方一，都是“高一尺，方一尺”，連同原有小黑立方一，總計三立方。在這三立方中，黑立方居二，赤立方居一，也就是屬於陽馬者二，而屬於鱉臑者則一；即兩份鱉臑體積相當於一份陽馬體積；即是“每二分鱉臑則一陽馬也”。此外尚有小赤鱉臑二與小黑陽馬二, 可拼接成“小赤一黑塹堵”二，這兩個“小赤一黑塹堵”，又可拼接成小立方一;連同前面三立方，總計四立方;在這四立方中，得自陽馬或鱉臑的立方者居三，而得自與原“赤黑塹堵”相似的塹堵拼合成立方者則居一。劉徽認為，不拘如何改變這些模型的大小形狀，必有這種常然的關係，即“固有常然之勢也”。在前面所述三立方中，屬於黑陽馬者率居二，屬於赤鱉臑者率居一，即是“有一、二之別”；也就是“一、二之率定矣”。若再中分“小赤一黑塹堵”的廣、袤、高，其中四分之三是可以推算的。如果按照這樣分割下去，則“半之彌少，其餘彌細。至細日微，微則無形”。於是利用極限觀念即可證明了陽馬與鱉臑體積之比為二比一。劉徽在進行了一次分割之後，並沒有再次進行分割，而是按照“情推”的，也就是用極限觀念以及數學原理推導的。因而即是證明了“劉徽原理”的正確性。(如圖6、圖7)即
陽馬:鱉臑=2：1;
又依據陽馬與鱉臑體積之和，即
陽馬+鱉臑=1/2(長×寬×高)。
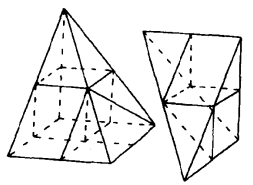圖6
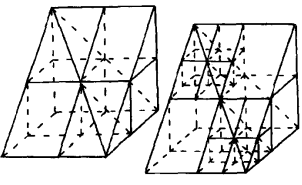圖2於是可得陽馬、鱉臑體積算法分別為:
陽馬體積=1/3 (長×寬×高);
鱉臑體積=1/6 (長×寬×高)。
以上所說，就是劉徽為了推證直線型立體的體積算法，利用三種基本幾何體，以及所創造的“劉徽原理”，從而為論證直線型立體的體積算法奠定了理論基礎。
