在數學分支的代數幾何中,塞爾對偶是存在於n維的非奇異代數變數V上的對偶(並且對於矢量束而言更加通用)。 它表明,上同調組H^i是另一個H^(n-i)的雙重空間。
基本介紹
- 中文名:塞爾對偶
- 外文名:Serre duality
- 學科:數學
- 本質:n維的非奇異代數變數V上的對偶
- 表明:一個上同調是另一個的雙重空間。
- 相關名詞:上同調
簡介,代數曲線,起源與泛化,
簡介
在數學分支的代數幾何中,塞爾對偶是存在於n維的非奇異代數變數V上的對偶(並且對於矢量束而言更加通用)。 它表明,上同調組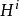 是另一個
是另一個 的雙重空間。
的雙重空間。
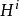

在平滑緊湊複雜流形V上的全向矢束E的情況下,語句的形式為:
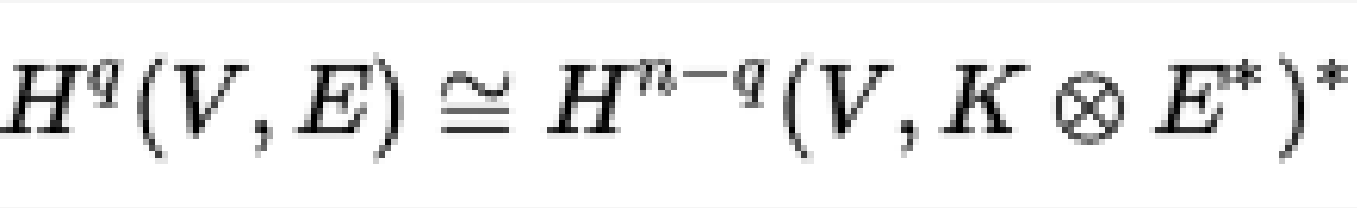
其中V不一定是投影。
代數曲線
代數曲線的情況已經在黎曼聖洛克定理中被隱含了。 對於曲線C,在i> 1上連貫組Hi消失; 但H1確實進入隱含。 事實上,定理的基本關係涉及l(D)和l(K-D),其中D是除數,K是規範類的除數。 在塞爾之後,我們將l(K-D)認為是H1(D)的維數,其中現在D表示由除數D確定的線束。也就是說,在這種情況下,塞爾對偶關係組H1(D)和H0(KD*),我們正在讀取維度(符號:K是規範線束,D*是雙線束,並置是線束的張量乘積)。
在這個公式中,黎曼聖洛克定理可以被看作是一個計算歐拉的特徵函式h0(D)-h1(D),在曲線的屬性方面,H1(C,OC)和D的程度。這個表達式可以推廣到更高的維度。
因此,曲線的二元性是非常古典的;但它有一個有趣的光線投射。 例如,在黎曼表面理論中,複雜結構的變形理論通過二次微分(即L(K2)的截面)進行了典型的研究。金田彥和D.C.Sspencer的變形理論通過H1(T)識別變形,其中T是切線束K*。 二元性表明為什麼這些方法相符合。
起源與泛化
理論的起源在於塞爾早期對幾個複雜變數的工作。 在亞歷山大·格羅登迪克的泛化中,塞爾二元性在更廣泛的環境中成為連貫二元性的一部分。 雖然K以上的作用在一般的塞爾對偶性中是由少量束的決定性線束髮揮的,但當V為多態時,完全一般性K在不存在V上的非奇異性假設的情況下不能僅僅是單個束完全一般性的表述使用派生類別和Ext函子,以允許K現在由鏈的複合體代表,即二元化複合體。 然而,定理的陳述是可以肯定的。
