基本介紹
- 中文名:塞爾伯格篩法
- 外文名:Selberg sieve
- 所屬學科:數學
- 所屬問題:初等數論(素數分布)
- 提出者:塞爾伯格
基本介紹,相關介紹,
基本介紹
塞爾伯格篩法是在數論中有廣泛套用的一個初等方法。設A是由有限個整數組成的集合(元素可以重複),P是由無限個素數組成的集合(元素不能重複),以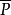 表示所有不屬於P的素數組成的集合,再設z≥2是任意實數,並令
表示所有不屬於P的素數組成的集合,再設z≥2是任意實數,並令
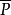
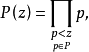
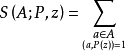
1.S(A;P,2)=|A| (|A|表示A中元素個數);
2.S(A;P,z)≥0;
3.S(A;P,z1)≥S(A;P,z2),2≤z1≤z2;
4.對任意的2≤ω≤z,有
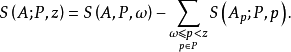
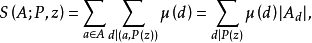
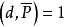
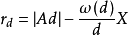

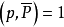
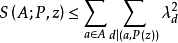
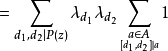
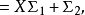
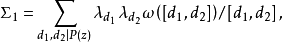
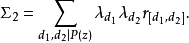
把X∑1稱為主項,∑2稱為餘項,由於當d≥ξ時λd=0,所以餘項∑2的項數不超過ξ2,這樣,通過對參數ξ的選擇就可控制餘項的階,使其低於主項的階而可以略去。同時還可選擇一組滿足所述條件的λd,使∑1最小而得到一個儘可能好的上界估計,這就是塞爾伯格的篩法。篩法的基本問題是估計篩函式S(A;P,z)的上界和正的下界。
相關介紹
篩法源於古希臘的埃拉托斯特尼(Eratosthenes),後經多次改進才形成今天的篩法。1950年,塞爾伯格(A.Selberg)在其論文“等差數列的初等證明”(參見“塞爾伯格漸近公式”)中利用求二次型極值的方法對埃拉托斯特尼篩法作了重大改進,由他的篩法可得到篩函式上界的估計,若與布赫什塔布恆等式相結合就可得到篩函式的下界估計,塞爾伯格篩法的重要套用如:1956年,王元套用它證明了(3+4);維諾格拉多夫(И.М.Виноградов)證明了(2+3);塞爾伯格證明了區間(A,A+N)中素數個數不超過2N/ln N+O(N ln ln Nln-2N),其中,O中常數與A無關;對固定常數0<δ<1,則證明了在算術級數kn+l(n=1,2,…)中不超過x的素數個數不大於
2x(φ(k)ln x/k)-1+O(x ln ln x ln-2x).
目前許多好結果,幾乎都是利用加權形式的塞爾伯格篩法得到的。
塞爾伯格(Selberg,Atle,1917.6.14-)是挪威一美國數學家。挪威科學院及美國科學藝術研究院院士。 他第一次用初等方法證明了素數分布定理,提出了後以他名字命名的塞爾伯格篩法。由於他在數論研究上的傑出貢獻,而榮獲1950年菲爾茲獎。塞爾伯格的研究領域廣泛,並不斷開拓新的研究方向。在二十世紀的數學史上以他的名字命名的還有塞爾伯格等式,塞爾伯格不等式,塞爾伯格漸近公式,塞爾伯格猜想,塞爾伯格函式等等。

