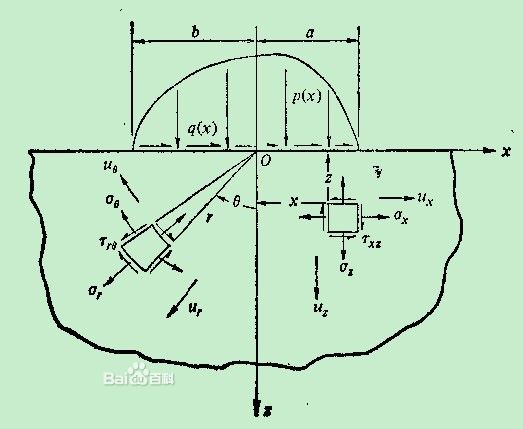
基礎振動半空間理論

基礎振動半空間理論是將基礎看做剛體，置於半空間的表面上。將土壤看做半無限的彈性體，在剛體上作用著靜力荷載和動力荷載。此問題可分解為兩個問題的疊加來求解：在靜力荷載作用下剛體壓於半空間的問題；在動力荷載作用下剛體的振動問題以及半空間各點的位移和應力問題。

基本介紹

• 中文名：基礎振動半空間理論
• 外文名：elastic half-space theory of foundation vibration
• 學科：工程力學
• 荷載：周期性變化荷載和衝擊荷載
• 假設：半空間是均質、連續、各向同性
• 模型：剛體一半空間模型

定義

基礎振動半空間理論通常採用的基本假定是半空間是均質、連續、各向同性、線性變形的彈性體。此外還假定：體力略去不計；材料阻尼（彈性體的內阻尼）略去不計；在壓模(基底)與半空間之間相互作用的摩擦力略去不計，即基底光滑，對基底下面的半空間各點的徑向位移不起阻礙作用。採用這些假定的理論一般稱為精確理論，而為了進一步簡化再附加其他假定的理論則稱為近似理論。根據所採用的力學模型，各種計算理論可分為幾種類型：質量一彈簧一阻尼器模型。採用此模型的理論簡稱為質彈阻理論或彈簧理論。剛體一半空間模型採用此模型的理論簡稱為半空間理論。其中研究得比較成熟的是均質、連續、各向同性、線性變形的彈性半空間模型。剛體一彈性層模型彈性層置於絕對堅硬的基岩上。其中研究得較多的是具有有限厚度的單層理想彈性層模型。

地基模型

土—結構動力相互作用就是波動在結構。地基系統內傳播時引起的結構和地基的動力反應問題。在土—結構動力相互作用的研究中選擇既符合實際情況又便於計算的地基模型是問題的關鍵所在。嚴格地說，無論是土質地基或岩石地基，它們都屬於非線性材料。近年來，在土力學中己發展了多種土的非線性模式，但是由於問題的複雜性，要將現有的多種土的非線性模式用於土一結構動力相互作用分析仍有很大的困難。土—結構動力相互作用研究仍多限於線彈性、粘彈性或等效線性假設的基礎之上進行。分析土—結構動力相互作用的地基模型中，套用最廣泛的是Winkler模型和彈性半空間模型。在Winkler模型中，由於採用Winkler假設而使計算大為簡化。但Winkler模型不能反映地基變形的連續性，因而不能全面考慮結構與彈性介質的相互作用。彈性半空間模型將地基理想為各向同性的均勻彈性半無限體，克服了Winkler模型的缺陷，基於此模型所獲得的研究成果得到普遍套用。但實際地基並不是理想的半無限體，大多數地基並不是各向同性均質的。如天然地基常由不同地質時期沉積的土層組成,不同的土層具有不同的物理力學特徵和結構特徵：實際上土的橫向模量往往不同於豎向模量。自60年代以來，土骨架是一種各向異性體這一事實已逐漸成為岩土工程界的共識。Simons，King等許多學者認為成層均勻的橫觀各向同性的彈性半空間可以表示範圍廣泛的地基，採用橫觀各向同性彈性體模擬場地更接近實際。近十餘年來，許多研究者對橫觀各向同性層狀彈性體的動力回響進行了研究，其中Wass等人已提出了一套完整的分析方法，並廣為套用。實際天然土體是複雜的二相介質體系，其中十顆粒形成土骨架，骨架孔隙中充滿流體和氣體。三相之間物理和化學成分的不同組合使土體具有不同的性狀。當固體土骨架之間孔隙中充滿流體，則形成飽和土，它實際上是一種流體飽和的多孔介質。自1971年Lcuo等全面總結了單相彈性介質半空間體上剛性基礎的各類振動特性以來，國內外一些學者將其注意力轉入了對多孔飽和介質地基模型的研究,以期反映飽和地基中孔隙水的影響。

計算方法

直接法

直接法就是將地基與結構作為一個完整的系統進行分析，這種方法可以同時得到地基反應和結構反應。當採用時域逐步積分時，可以考慮地基土的非線性。由於直接法的分析模型自由度多，計算量大，針對簡單的邊界條件和均質(或簡單層狀)介質，可獲得解析解答，在一般情況下，多採用數值法或半解析數值法。常用的數值法或半解析數值法有：有限單元法;邊界單元法；無限元法和有限條(層)法等。

有限單元法

由於有限單元法套用靈活，通用性強，在土一結構動力相互作用研究上得到比較廣泛的套用。有限元解法又可以分為兩大類：頻域有限元法和時域有限元法。頻域有限元法是將對應於不同頻率的穩態波解疊加，得到時域內的波動過程，既可直接用輸入波頻譜求解，也可通過傳遞函式過渡求解。但頻域解法要求計算模型只能是線彈性或粘彈性。一般情況下用時域有限元法解波動方程最為直接，可以很好地模擬波動的傳播過程。應注意到，用有限單元法計算土一結構動力相互作用其缺點也是明顯的：對於真實的介質和場地地形等條件，結構地震計算都需要劃分相當多的單元，這時，剛度陣、質量陣所占的存儲空間是相當可觀的，所需要的計算機記憶體和機時往往大到現有中、小型計算機無法實現的地步：另外，採用有限單元法無法模擬無限地基的輻射阻尼而必須引入人工邊界。

邊界元法

邊界元法是利用Geren公式，利用基本解將支配物理現象的域內微分方程轉換為邊界積分方程，然後在邊界上離散進行數值求解。由於邊界元自動滿足遠場的輻射條件，無需引入人工邊界，在求解地基動力剛度和基礎回響、地形對地震波的散射效應以及地下結的動力回響等方面得到廣泛的套用。但對於複雜介質地基，尋求問題的基本解是十分困難的。

有限條法

有限條(層)法是由Y.K.Cheung提出的一種半解析數值方法，其基本思想是在結構或介質的一個方向上採用有限元，邊界元或其它離散單元，而另一個方向或兩個方向上採用解析方法，例如級數展開法。由於有限條(層)法只適用於規則的成層地基，同時需截取很大的地基範圍，限制了該方法的廣泛套用。

集中參數法

集中參數法將半無限地基模擬為彈簧一阻尼一質量系統用以土一結構動力相互作用分析。這種方法概念明確，套用方便，在工程中具有廣泛的套用前景。但對於非均勻、非線性或地形變化較大的複雜地基而言，集中參數法不再適用。