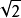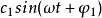定義
jībō
〖fundamentalwave〗
複合波的最低頻率分量。
在複雜的周期性振盪中,包含基波和
諧波。和該振盪最長周期相等的正弦波分量稱為基波。相應於這個周期的頻率稱為
基本頻率。頻率等於基本頻率的整倍數的正弦波分量稱為諧波。
周期信號分析
一個周期信號可以通過
傅立葉變換分解為直流分量c0和不同頻率的正弦信號的線性疊加:
其中,cm表示m次
諧波的幅值,其
角頻率為mω,初始相位為φm,其
有效值為cm/
。
當m=1時,
為
基波分量的表達式,其角頻率為ω,初始相位為φ1,其方均根值c1/
稱為基波有效值。
ω/2π為基波分量的頻率,稱為基波頻率,基波分量的頻率等於交流信號的頻率。而m次諧波的頻率為基波頻率的整數倍(m倍)。
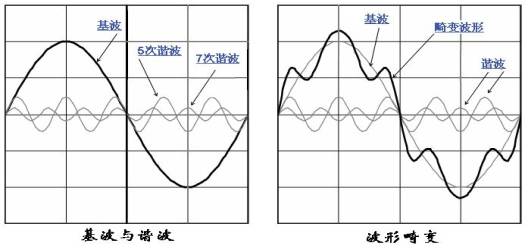 基波與諧波
基波與諧波測量方法
濾波法
當信號的諧波頻率與基波頻率差距較大時,即信號的低次諧波含量較小,主要為高次諧波時,可以通過低通濾波的方法將高次諧波濾除,剩下就是信號的基波,採用均值檢波表、峰值檢波表和真有效值檢波表均可測量其有效值,測量結果近似等於基波有效值。
常用濾波器有:
巴特沃斯濾波器
巴特沃斯濾波器具有較平坦的通帶。
貝塞爾濾波器
貝塞爾濾波器具有較高線性度的相角位移。
切貝雪夫濾波器
切貝雪夫濾波器具有較陡峭的過渡帶。
當諧波頻率與基波頻率差距較小時,可採用切比雪夫濾波器或高階的巴特沃斯濾波器。
傅立葉變換
原理
基波函式可由幅值,角頻率和初相位來唯一確定,即Asin(ωt+φ),展開後可以寫成
其中:a1cos(ωti)+a2sin(ωti)是估計得到的基波信號在第i點的值;f(ti)是被估計信號在第i點的值,即輸入信號的採樣值,它含有基波和諧波成分;n為估計所用的點數;λ為加權係數,可根據回響時間和估計精度來選取,一般在0.95到1之間。
根據求多元函式極值的必要條件,有
其中:
相應的時間遞推公式為
解式(2),得到a1和a2,代入a1cos(ωtk)+a2sin(ωtk)中即得到估計的基波信號瞬時值,同時,由可以得到基波幅值,由φ=arctg(a1/a2)可以得到初相位。
在上面的計算中,Satons假定估計的基波頻率是ω0,例如50Hz,如果它等於實際信號中的基波頻率ωs,那么得到的φ角是常數。如果兩者不等,就會產生相應的角度差對一定的Δw,隨著時間的推移Δφ就會在-π和π間以斜率為Δw呈鋸齒形變化。也就是說,φ的變化反映了估計的頻率與實際頻率的關係,於是可以通過一個比例積分調節器ws=w0+(kp+ ki/s)Δφ來調整估計的基波頻率,達到頻率跟蹤、改善估計效果的目的。通過估計的基波頻率和初相位,就可以得到基波的相角ωt+φ,它可以用作系統的同步信號。圖1是基波提取方法的計算流程圖,利用該流程圖可以很方便地實現所提出的信號處理方法。
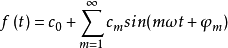
 基波與諧波
基波與諧波