《基於頻域分析方法的對偶四元數捷聯慣導方法》是東南大學於2010年4月23日申請的專利，該專利的申請號為2010101539073，公布號為CN101825468A，授權公布日為2010年9月8日，發明人是陳熙源、陳建鋒、方琳、申沖、祝雪芬。
《基於頻域分析方法的對偶四元數捷聯慣導方法》針對傳統的時域捷聯慣導算法由於對載體的角速度和比力進行多項式擬合而導致的不能充分補償載體運動的各種誤差的問題進行設計，運用頻域分析方法對慣導器件輸出的增量信號和解算過程中得到的導航信息進行光滑延拓以及離散傅立葉變換，並利用頻域內實現的對偶四元數捷聯慣導算法對變換得到的頻譜信號進行解算，最後對解算得到的信號進行傅立葉反變換以得到時域內的導航解。
2013年，《基於頻域分析方法的對偶四元數捷聯慣導方法》獲得第八屆江蘇省專利項目獎優秀獎。
（概述圖為《基於頻域分析方法的對偶四元數捷聯慣導方法》摘要附圖）
基本介紹
- 中文名：基於頻域分析方法的對偶四元數捷聯慣導方法
- 公布號：CN101825468A
- 公布日：2010年9月8日
- 申請號：2010101539073
- 申請日：2010年4月23日
- 申請人：東南大學
- 地址：江蘇省南京市四牌樓2號
- 發明人：陳熙源、陳建鋒、方琳、申沖、祝雪芬
- Int.Cl.：G01C21/16（2006.01）I、G01C21/20（2006.01）I
- 代理機構：南京經緯專利商標代理有限公司
- 代理人：許方
- 類別：發明專利
專利背景,發明內容,專利目的,技術方案,改善效果,附圖說明,技術領域,權利要求,實施方式,榮譽表彰,
專利背景
自20世紀50年代末捷聯慣導系統的概念提出以來，經過50多年的發展，捷聯慣導系統已經廣泛套用于軍用、民用的多個領域，但是在精度、可靠性等方面還存在著不少的問題。總的來說，捷聯慣導系統性能的提高主要依賴於兩個方面：高精度的慣導器件和理想的導航算法。近20年來，各種精度的慣導器件的發展取得了長足的進步，而捷聯慣導算法的發展卻仍然局限於對原有算法作局部的改進。2005年，有學者系統地提出了一種基於對偶四元數代數的捷聯慣導算法。與成熟的捷聯慣導算法相比，其精度有了一定程度的提高，而算法的整體結構也出現了較大的改變，具體體現在：採用對偶四元數這種數學工具統一表示轉動和平移，使算法模擬的剛體運動更加接近於實際運載體的運動。但是，不管是這種基於對偶四元數代數的捷聯慣導算法還是傳統的將轉動和平移分開表示的捷聯慣導算法，採用的都是根據預積分得到的慣導器件輸出的增量信號直接在時域內對載體的角速度和比力進行多項式擬合以補償載體運動的各種誤差的思想。這種思想本身就是近似的，因為載體的運動具有很大的隨機性，角速度和比力的變化是十分複雜的。
在一定條件下，採用頻域分析方法對慣導器件輸出的增量信號進行重構，能夠復現原信號。利用頻域內實現的對偶四元數捷聯慣導算法對重構後的信號進行解算，可以彌補傳統的時域捷聯慣導算法的缺陷，進一步提高算法的精度，特別適用於高動態環境。
發明內容
專利目的
《基於頻域分析方法的對偶四元數捷聯慣導方法》針對傳統的時域捷聯慣導算法由於對載體的角速度和比力進行多項式擬合而導致的不能充分補償載體運動的各種誤差的問題進行設計，目的在於提高捷聯慣導系統在高動態環境下的精度，結合已有時域對偶四元數捷聯慣導算法精度高的特點，提出了一種基於頻域分析方法的對偶四元數捷聯慣導算法，適用於中高精度的導航系統及定位、定向系統等。
技術方案
《基於頻域分析方法的對偶四元數捷聯慣導方法》包括以下步驟：
（1）在頻域內求解對偶四元數
的運動學方程並求取推力速度；
（2）在頻域內求解對偶四元數
的運動學方程並求取引力速度；
（3）計算載體在地球坐標系中的速度向量；
（4）在頻域內求解對偶四元數
的運動學方程；
（5）計算載體在地球坐標系中的位置向量；
（6）計算載體的姿態和航向。
其中的對偶四元數、、分別表示推力速度坐標系T、引力速度坐標系G、位置坐標系U相對於慣性坐標系I的一般性剛體運動。
優選地，步驟（1）中所述的頻域內的運動學方程的求解方法如下：首先對角增量和速度增量進行光滑延拓即用
的補償信號表示角增量和速度增量的補償信號；然後對得到的角增量和速度增量信號進行離散傅立葉變換，並根據頻域內的角速度和角增量、加速度和速度增量的對應關係得到旋量
的頻譜幅值；再根據頻域內的運動學方程以及初始條件求解的頻譜幅值，初始條件也要轉化為頻域內的形式；最後用得到的的頻譜幅值替換頻域形式的初始條件，完成對偶四元數的更新；其中表示tn時刻的對偶四元數，旋量是推力速度坐標系T下由角速度和加速度構成的對偶向量。
優選地，步驟（2）中所述的頻域內對偶四元數的運動學方程的求解方法如下：首先根據頻域形式的地球自轉角速度以及重力的頻譜幅值構造旋量
的頻譜幅值；然後根據頻域內的運動學方程以及初始條件求解的頻譜幅值，其中的初始條件也要轉化為頻域內的形式；最後用得到的的頻譜幅值替換頻域形式的初始條件，完成對偶四元數的的更新；其中，旋量是引力速度坐標系G下由角速度和加速度構成的對偶向量。
優選地，步驟（3）中所述的載體在地球坐標系中的速度向量的計算方法為：根據載體在地球坐標系中的速度表達式
的頻域形式計算載體在地球坐標系中的速度的頻譜幅值，其中的推力速度
、引力速度
以及載體在地球坐標系中的位置向量r都要採用頻域內的表達形式；對得到的頻譜幅值進行傅立葉反變換可以得到時域內載體在地球坐標系中的速度向量；其中，四元數qIG為對偶四元數的實數部分，四元數qIG為四元數qIG的共軛形式，ωIG為旋量的實數部分，運算符“о”表示四元數乘運算。
優選地，步驟（4）中所述的頻域內的運動學方程的求解方法為：首先根據頻域形式的地球自轉角速度以及推力速度和引力速度的頻譜幅值構造旋量
的頻譜幅值；然後根據頻域內的運動學方程以及初始條件求解的頻譜幅值；最後用得到的的頻譜幅值替換頻域形式的初始條件，完成對偶四元數的更新；其中的旋量是位置坐標系U下由角速度和速度構成的對偶向量。
優選地，步驟（5）中所述的載體在地球坐標系中的位置向量的計算方法為：根據載體在地球坐標系中的位置向量表達式
的頻域形式求取位置向量的頻譜幅值，並在此基礎上更新步驟（3）中用到的頻域形式的位置向量
，同時在頻域內計算重力以完成對重力的頻譜幅值的更新；最後對得到的位置向量的頻譜幅值進行傅立葉反變換就可以得到時域內載體在地球坐標系中的位置向量；其中，
為對偶四元數的共軛形式，
為對偶四元數的實數部分，
為對偶四元數的對偶部分。
優選地，步驟（6）中所述的載體的姿態和航向的計算方法為：套用遞推算法將地球坐標系下的位置矢量轉化為導航系即地理坐標系下的位置參數即緯度L、經度λ和高度h，並根據位置參數計算地球坐標系相對導航系的旋轉四元數I
；然後求取載體坐標系相對導航系的旋轉四元數
以確定載體的姿態和航向，其中載體坐標系相對慣性坐標系、地球坐標系相對慣性坐標系的旋轉四元數
、
可以根據關係式
求取；其中，四元數
表示對偶四元數
的共軛形式。
《基於頻域分析方法的對偶四元數捷聯慣導方法》的原理：運用頻域分析方法對慣導器件輸出的增量信號和解算過程中得到的導航信息進行光滑延拓以及離散傅立葉變換，並利用頻域內實現的對偶四元數捷聯慣導算法對變換得到的頻譜信號進行解算，最後對解算得到的信號進行傅立葉反變換以得到時域內的導航解。
改善效果
（1）可以充分利用慣導器件輸出信號各個頻段的信息，更真實地反映慣導器件的輸出特性；
（2）有助於消除慣導器件（主要是陀螺）在某些頻段的噪聲，而這些噪聲是用傳統的時域方法無法有效消除的；
（3）能夠方便地實現捷聯慣導系統與衛星導航系統的匹配和算法融合，因為衛星導航系統中的很多算法都是在頻域內實現的；
（4）能夠彌補慣導器件精度的不足，提高捷聯慣導系統的整體精度，降低系統的整體成本。
附圖說明
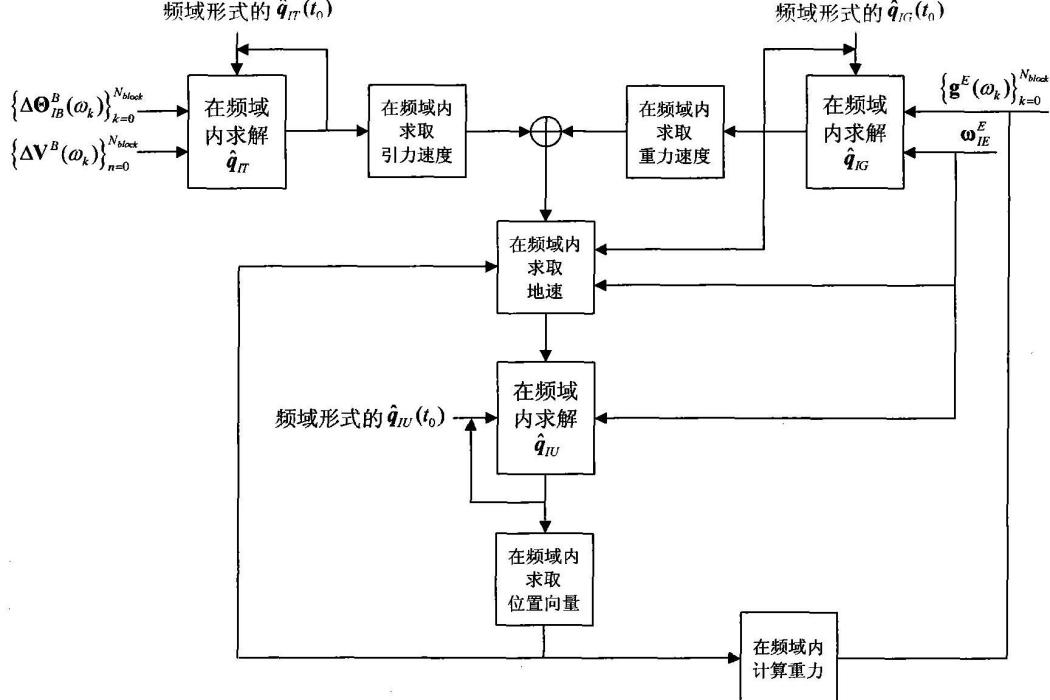
圖1為《基於頻域分析方法的對偶四元數捷聯慣導方法》的一種基於頻域分析方法的對偶四元數捷聯慣導算法的原理框圖；
圖2為在頻域內更新對偶四元數的原理示意圖；
圖3為在頻域內更新對偶四元數的原理示意圖；
圖4為在頻域內更新對偶四元數的原理示意圖。
技術領域
《基於頻域分析方法的對偶四元數捷聯慣導方法》屬於慣性導航技術領域，涉及一種捷聯慣導算法，特別涉及一種基於頻域分析方法的對偶四元數捷聯慣導算法，適用於高動態環境下中高精度的導航系統及定位、定向系統等。
權利要求
1. 《基於頻域分析方法的對偶四元數捷聯慣導方法》特徵在於包括以下步驟：
（1）在頻域內求解對偶四元數的運動學方程並求取推力速度；
（2）在頻域內求解對偶四元數的運動學方程並求取引力速度；
（3）計算載體在地球坐標系中的速度向量；
（4）在頻域內求解對偶四元數的運動學方程；
（5）計算載體在地球坐標系中的位置向量；
（6）計算載體的姿態和航向。
其中的對偶四元數、、分別表示推力速度坐標系T、引力速度坐標系G、位置坐標系U相對於慣性坐標系I的一般性剛體運動。
步驟（1）中所述的頻域內的運動學方程的求解方法如下：首先對角增量和速度增量進行光滑延拓即用的補償信號表示角增量和速度增量的補償信號；然後對得到的角增量和速度增量信號進行離散傅立葉變換，並根據頻域內的角速度和角增量、加速度和速度增量的對應關係得到旋量的頻譜幅值；再根據頻域內的運動學方程以及初始條件求解的頻譜幅值，初始條件也要轉化為頻域內的形式；最後用得到的的頻譜幅值替換頻域形式的初始條件，完成對偶四元數的更新；其中表示tn時刻的對偶四元數，旋量是推力速度坐標系T下由角速度和加速度構成的對偶向量。
步驟（2）中所述的頻域內對偶四元數的運動學方程的求解方法如下：首先根據頻域形式的地球自轉角速度以及重力的頻譜幅值構造旋量的頻譜幅值；然後根據頻域內的運動學方程以及初始條件求解的頻譜幅值，其中的初始條件也要轉化為頻域內的形式；最後用得到的的頻譜幅值替換頻域形式的初始條件，完成對偶四元數的的更新；其中，旋量是引力速度坐標系G下由角速度和加速度構成的對偶向量。
步驟（3）中所述的載體在地球坐標系中的速度向量的計算方法為：根據載體在地球坐標系中的速度表達式的頻域形式計算載體在地球坐標系中的速度的頻譜幅值，其中的推力速度、引力速度v以及載體在地球坐標系中的位置向量r都要採用頻域內的表達形式；對得到的頻譜幅值進行傅立葉反變換可以得到時域內載體在地球坐標系中的速度向量；其中，四元數qIG為對偶四元數的實數部分，四元數qIG為四元數qIG的共軛形式，ωIG為旋量的實數部分，運算符“о”表示四元數乘運算。
步驟（4）中所述的頻域內的運動學方程的求解方法為：首先根據頻域形式的地球自轉角速度以及推力速度和引力速度的頻譜幅值構造旋量的頻譜幅值；然後根據頻域內的運動學方程以及初始條件求解的頻譜幅值；最後用得到的的頻譜幅值替換頻域形式的初始條件，完成對偶四元數的更新；其中的旋量是位置坐標系U下由角速度和速度構成的對偶向量。
步驟（5）中所述的載體在地球坐標系中的位置向量的計算方法為：根據載體在地球坐標系中的位置向量表達式的頻域形式求取位置向量的頻譜幅值，並在此基礎上更新步驟（3）中用到的頻域形式的位置向量，同時在頻域內計算重力以完成對重力的頻譜幅值的更新；最後對得到的位置向量的頻譜幅值進行傅立葉反變換就可以得到時域內載體在地球坐標系中的位置向量；其中，為對偶四元數的共軛形式，為對偶四元數的實數部分，為對偶四元數的對偶部分。
步驟（6）中所述的載體的姿態和航向的計算方法為：套用遞推算法將地球坐標系下的位置矢量轉化為導航系即地理坐標系下的位置參數即緯度L、經度λ和高度h，並根據位置參數計算地球坐標系相對導航系的旋轉四元數；然後求取載體坐標系相對導航系的旋轉四元數以確定載體的姿態和航向，其中載體坐標系相對慣性坐標系、地球坐標系相對慣性坐標系的旋轉四元數、可以根據關係式求取；其中，四元數表示對偶四元數的共軛形式。
實施方式
《基於頻域分析方法的對偶四元數捷聯慣導方法》的實現過程如圖1所示，主要包括以下六個步驟：
（1）在頻域內求解對偶四元數的運動學方程並求取推力速度
如圖2所示，首先對ΔθIB（tn）、Δv（tn）進行光滑延拓（前提是用的補償信號表示
、
的補償信號，其中表示tn時刻的對偶四元數，、表示
時刻慣導器件輸出的角增量和速度增量信號）；然後對得到的角增量和速度增量信號進行離散傅立葉變換得到、的頻譜幅值
、
，並根據頻域內的角速度和角增量、加速度和速度增量的對應關係得到旋量的頻譜幅值
；再根據頻域內的運動學方程以及對偶四元數的初值
的頻域形式求解的頻譜幅值
；最後用得到的的頻譜幅值替換頻域形式的，完成對偶四元數的更新。
推力速度的頻譜幅值可以根據推力速度表達式
的頻域形式求取。
（2）在頻域內求解對偶四元數的運動學方程並求取引力速度
如圖3所示，首先根據頻域形式的
以及
構造旋量的頻譜幅值
，其中的表示地球自轉角速度、表示重力的頻譜幅值；然後根據頻域內的運動學方程以及對偶四元數的初值
的頻域形式求解的頻譜幅值
；最後用得到的的頻譜幅值替換頻域形式的，完成對偶四元數的更新。
引力速度的頻譜幅值可以根據引力速度表達式
的頻域形式求取。
（3）計算載體在地球坐標系中的速度向量
根據載體在地球坐標系中的速度表達式的頻域形式計算載體在地球坐標系中的速度的頻譜幅值，其中的推力速度、引力速度以及載體在地球坐標系中的位置向量都要採用頻域內的表達形式；對得到的頻譜幅值進行傅立葉反變換可以得到時域內載體在地球坐標系中的速度向量。
（4）在頻域內求解對偶四元數的運動學方程
如圖4所示，首先根據頻域形式的以及推力速度和引力速度的頻譜幅值構造旋量的頻譜幅值
，然後根據頻域內的運動學方程以及對偶四元數的初值
的頻域形式求解的頻譜幅值
；最後用得到的的頻譜幅值替換頻域形式的，完成對偶四元數的更新。
（5）計算載體在地球坐標系中的位置向量
根據載體在地球坐標系中的位置向量表達式的頻域形式求取位置向量的頻譜幅值，並在此基礎上更新步驟（3）中用到的頻域形式的位置向量，同時在頻域內計算重力以完成對重力的頻譜幅值的更新；時域內載體在地球坐標系中的位置向量可以通過對位置向量的頻譜幅值進行傅立葉反變換得到。
（6）計算載體的姿態和航向
套用遞推算法將地球坐標系下的位置矢量轉化為導航系（地理坐標系）下的位置參數（緯度L、經度λ和高度h），並在此基礎上計算地球坐標系相對導航系的旋轉四元數；然後求取載體坐標系相對導航系的旋轉四元數以確定載體的姿態和航向，其中載體坐標系相對慣性坐標系、地球坐標系相對慣性坐標系的旋轉四元數、可以根據關係式
、
求取。
榮譽表彰
2013年，《基於頻域分析方法的對偶四元數捷聯慣導方法》獲得第八屆江蘇省專利項目獎優秀獎。
