基於等效電路模型的諧波源定位

諧波源定位過程中，在公共連線點（point of common coupling，PCC）處把系統等效為兩個部分, 即供電側U(utility)和用戶側C (customer), 然後根據相應的等效電路模型, 通過功率定位法、臨界阻抗定位法、靈敏度定位法等確定出是主諧波源的一側, 稱之為基於等效電路模型的定位法。

基本介紹

• 中文名：基於等效電路模型的諧波源定位
• 外文名：Harmonic Source Location Based on Equivalent Circuit Model
• 定位目的：分析諧波狀態
• 定位方法：功率法、臨界阻抗法、靈敏度法
• 基本結構：系統運行三相平衡狀態下
• 其他方法：諧波狀態估計定位法

諧波源定位的意義

隨著電網中非線性負荷的不斷增多, 電力系統中的諧波污染問題變得日益嚴重, 給電網的經濟運行及用戶的安全用電造成了極大的影響。為了及時解決電網中諧波治理課題, 達到準確分清諧波責任, 簡單有效的治理目的, 必須先明確電力系統中的諧波分布或諧波狀態。

分析諧波狀態, 首先要了解諧波源的位置。如果諧波源的位置已知, 那么電網中的諧波分布就成為諧波的傳播與擴散問題, 也就是諧波潮流問題。但隨著電網規模的增大,實際系統中諧波源的位置存在不確定性, 仍然用潮流方法來分析諧波的擴散與滲透, 就會失去分析的主體。所以, 在諧波源的位置未知的情況下, 要對諧波影響進行分析, 就需要對諧波源進行定位。

基於等效電路模型的定位法

系統的Norton(諾頓)等效電路模型如圖1所示:

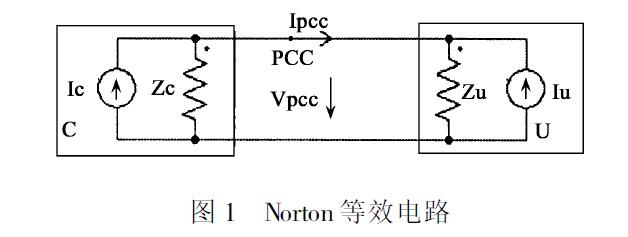圖1 諾頓等效模型

通過等效變換得到的Thevenin(戴維南)等效電路模型如圖2所示：

圖2 戴維南等效電路

圖中所示的PCC 點是公共電氣耦合點。根據不同的定位依據, 又可以分為功率定位法, 阻抗定位法, 靈敏度定位法。

功率定位法

功率定位法又可分為有功功率定位法和無功功率定位法。

有功功率定位法：

有功功率定位法是工程上最常用的定位方法。其主要思想是:在PCC 點處測量各次諧波的電壓和電流, 然後根據公式:

Pcc=Re(Vpcc* Ipcc)=Vpcc *Ipcc *cos (θvpcc -θipcc)

來判定諧波源的位置。如圖1中所示, 功率的正方向是從用戶側到供電側, 若P pcc >0 , 那么用戶側就是主諧波源;Ppcc <0 , 那么供電側就是主諧波源。從公式可以知道, 諧波源的判定不受相位差的影響 。

由於有功功率法比較直觀明了, 一直得到廣泛的套用。文獻[ 5 , 9] 指出諧波源的判定應由公共耦合點兩側的等效諧波電壓源幅值大小決定, 如圖2所示。此時,

P=EuEc*sinδ/(Zc+Zu)

諧波源的判定受到諧波源之間相位差的影響.這是因為在複雜的電力系統中, 有的諧波源可能會吸收諧波, 所以該法用於諧波源定位時可能會產生較大誤差。

無功功率定位法：

Q =Im*(Eu -Ec)*Eu / -j(Xu +Xc)= Eu*(Eu -Ec cosδ) /(Xu +X c)

從該公式可以看出, 無功功率的正負與阻抗的正負以及Eu -Eccosδ的正負有關。一般來說, 在基波情況下, 系統中的阻抗為正值, 但在諧波存在的情況下可能出現負值。現假定阻抗為正值, 如果Q <0 , 那么可以得到Eu <Ec , 如果Q >0 , 那么就不能判定Eu 和Ec 的大小, 從而不能判定諧波源的位置。所以無功功率定位法的準確度比較低。

臨界阻抗法

由於無功功率不能解決Q >0 時的定位問題,Chun Li, Wilsun Xu提出了“臨界阻抗法” ，計算由供電側發出的諧波無功功率被完全吸收所需的系統阻抗值X，也就是臨界阻抗係數X =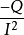 = 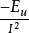sinθ, (其中θ是阻抗角), 然後比較 X 與(Xu +Xc) 2 的大小, 如果 X >(Xu +Xc) 2 , 那么供電側是主諧波源;反之, 用戶側是主諧波源。

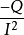
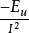
從上面的方程可以看出, 該法涉及到系統阻抗的測量, 由於實際電力系統的負荷波動比較大, 所以該法在實際中的套用受到一定的限制。

靈敏度定位法

近年來, 又有基於等效模型的諧波源定位新方法出現, 文獻就提出了一種靈敏度定位的方法。文中推導出電壓比率 θ=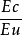 =(Z+Zc)/(Z+Zu), Z=Z* 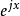=Vpcc /Ipcc，然後定義靈敏度Sx=∆θ/θ*∆X/X, 這裡的變數X 分別取Z , Zc , Zu , α, αc , αu , 也就是求出SZ 、SZc 、SZu 、Sα 、Sαc 、Sαu , 畫出靈敏度指數圖。其中αc ,αu 分別是用戶側和供電側的阻抗角。

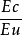
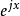
根據靈敏度指數圖, 如果靈敏度指數 ∣SZc ∣,∣Sαc∣在θ>1 時的值比∣ SZc ∣,∣ Sαc∣在θ<1 時的值小, 那么用戶側是主諧波源。如果靈敏度指數∣SZu∣ , ∣Sαu∣在θ<1 時的值比∣ SZu∣ , ∣Sαu∣在θ>1時的值小, 那么供電側是主諧波源。

利用靈敏度來定位, 就不用精確地測量系統的阻抗, 對系統阻抗測量有較大誤差時, 對於諧波源的判定依然保持很高的準確度。

此外，國內外科技工作者對諧波源定位做出了可貴的探索，還提出了微分方程法、基於最小二乘辨識的諧波源識別方法、基於GPS技術的諧波源檢測方法等。