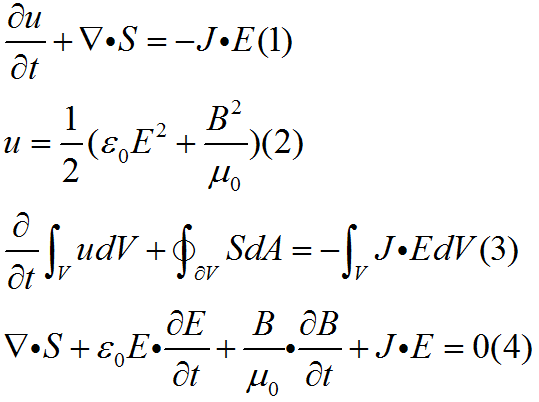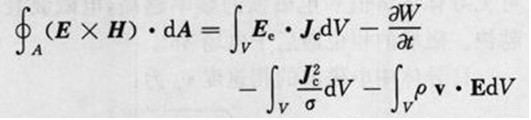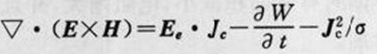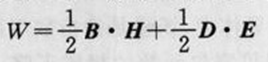坡印廷定理，英文表示Poynting theorem，是1884年約翰·坡印亭（John Poynting）提出的關於電磁場能量守恆的定理。他認為電磁場中的電場強度E與磁場強度H叉乘所得的矢量,即E×H=S，代表電磁場能流密度，表示一個與垂直通過單位面積的功率相關的矢量。人們稱這個矢量S為坡印廷矢量。坡印廷定理表明，在電磁場中的任意閉合面上，坡印廷矢量的外法向分量的閉面積分，等於閉合面所包圍的體積中所儲存的電場能和磁場能的時間減少率減去容積中轉化為熱能的電能耗散率。
基本介紹
- 中文名：坡印廷定理
- 外文名：Poynting theorem
- 提出人：約翰·坡印亭
- 提出時間：1884
推導,公式,公式形式,1、積分形式的坡印廷定理,2、微分形式的坡印廷定理,再思考,
推導
坡印廷定理是根據麥克斯韋方程組（包含法拉第電磁感應定律及改進的安培定律等）推導出來的。
首先考慮法拉第電磁感應定律（公式5），對其兩邊取B的點積得公式6；然後利用改進的安培定律（公式7），對其兩邊取與E的點積，得公式8。然後將等式（8）減去（6）並將恆等式（9）帶入，得到等式（10）。由於坡印廷矢量S定義為公式（11），帶入（10）化簡就可以得到等式（4）。這就推導出了表征電磁能量守恆關係的坡印廷定理。
公式
坡印廷定理的微分形式參見公式（1），式中S是坡印廷矢量，表示能量的流動；J是電流密度；E是電場強度。真空中的能量密度u的表達式參見公式（2），式中ε0是真空電導率，μ0是真空磁導率。由於電場不做功，（1）式的右端便給出了電磁場每秒·立方米所做的總功的負值。
坡印廷定理的積分形式參見式（3）,dV是包圍著體積V的曲面。
在工程領域，該定理通常寫成將能量密度u展開的形式，參見公式（4），這與流體力學的連續性方程相似。
公式形式
1、積分形式的坡印廷定理
對於由閉合曲面A所限定的體積V，有：
這就是電源外區域的、積分形式的坡印廷定理。它的含義是：垂直穿過閉合面A進入體積V的功率，等於體積內電磁儲能的增長率與由傳導電流Jc引起的功率損耗之和。更一般的情況是：
式中Ec為電源中的局外場強，Jc為傳導電流，σ為體積V內介質的電導率，ρ為運動電荷的電荷密度，v為該電荷的運動速度，E=Jc/σ-Ee為總場強。整個方程的含義是：外源提供的功率等於體積v內電磁能量的增加率、傳導電流的功率損耗、運動電荷作功耗損的功率、垂直穿過曲面A向外界輸送的功率之總和。
2、微分形式的坡印廷定理
這是就場中某一點而言的。式中
再思考
對坡印廷定理的再思考：
我們這裡討論的直流電是指不隨時間變化的穩恆電流。在這種情況下，公式(1)中右邊第2項的位移電流為0。於是公式(1)成為安培定律的經典形式：
∇ × H = j c(8)
公式(8)的微分形式來源於安培定律的積分形式：通電導線的周圍有環形磁場。而電流以及傳導電流密度jc是由電池的電動勢驅動導線中的大量電子產生的。使用E點積方程(8)的兩邊，
E ⋅ ∇ × H = E ⋅ j c (9)
從物理意義上說，方程(9)的右邊代表導線內部的電功率密度，方程(9)左邊物理意義是不明確的。它究竟是代表導線內部的物理量還是導線外部的物理量？如果它是代表導線外部的物理量，jc = 0，方程(9)左邊也是0。如果它是代表導線內部的物理量，那么方程(9)左邊的H不能代表通電導線周圍的環形磁場。
由方程(9)，我們注意到：在直流電路的情況下，上一節推導出的坡印亭矢量只是一個數學定義。它在直流電路沒有形成真正的能流。圖1顯示的大學電磁學教課書的觀點：“認為電能是在導線外部通過坡印亭矢量傳輸到電路內部的觀點”，是不正確的。
庫侖靜電場是縱向電場。在直流電路中，金屬線中的電場也是縱向電場。雖然這兩個電場有一些相似之處，但事實上電源是有差別的。庫侖靜電場的電源是孤立電荷，直流電路的電源是電池，電池通過金屬線連線到負載電阻器。
在直流電路的情況下，通電導線邊界處的電場的邊界條件並不清楚的，是否存在淨電荷也是不明確的。由於靜電場可以用金屬蓋禁止，所以我們對於直流電路做了一些測試。在直流電路中，我們串聯一個電流表。1) 我們用金屬蓋禁止電池；2) 我們用金屬蓋禁止電阻器；3) 我們使用同軸電纜禁止內部電線。結果如下：電流表的讀數基本相同(精度為4位)。這些測試表明，在直流電路中，外部電場(包括金屬線界面附近的外部電場)的分布對金屬線內的電場基本上沒有影響。
總之，直流電能的傳輸過程與位移電流無關，所以也與坡印亭定理無關。在直流電路的情況下，電路內部的大量自由電子在電源的電動勢的驅動下運動，電動勢能轉化為自由電子動能，形成了電流。在這種情況下，坡印亭矢量只是一個數學定義，它沒有形成真正的能流，所以電磁能流不是從金屬導線的外部傳輸到內部的。也就是說，直流電能完全是在通電導線的內部傳輸的。
在推導坡印亭定理的過程中，從方程(4)到方程(5)，用到了法拉第定律。這個過程說明必須有個交變磁場產生交變電場的物理過程。這個過程在自由空間以及絕緣介質中的電磁波存在。
另外，當用上述經典的微分運算元把E的點積代入方程(1)的兩邊進行運算時，我們必須考慮我們採取微分運算的局部微小點在哪裡。如果這個局部微小點在導線之外，則傳導電流密度jc為零，這時坡印亭定理(7)退化為：
− ∇ ⋅ ( E × H ) = ∂ ∂ t ( ε E 2 2 + μ H 2 2 ) (10)
方程(10)僅僅是方程(7)的一個特例，其中傳導電流密度jc是零。方程(10)反映了電磁波在自由空間以及絕緣介質的傳輸過程。在直流電路的情況，導線外的電場強度以及電場強度都不隨時間變化，方程(10)的右邊為0；左邊坡印亭矢量的散度是0。
另一方面，如果局部微小點位於導線內部，則傳導電流密度jc和E在不同位置可能是不同的。更加重要的關鍵點：我們必須從物理源頭上搞清楚，導線內部的電場強度E和傳導電流密度jc是如何產生的。這個過程需要區分二種不同的情況：
1) 如果它們是由閉合電路中電源的電動勢產生的，那么這個物理過程不涉及到交變磁場產生交變電場，也就不涉及坡印亭定理。
2) 如果是電磁波傳輸到接收天線，在接收天線的導線內產生了電場強度E和電流密度j，那么這個物理過程需要坡印亭定理。所以，坡印亭定理(7)是有一定適用範圍的。
