基本介紹
- 中文名:坡印亭定理
- 外文名:Poynting theorem
- 別稱:坡印廷定理
- 提出者:約翰·坡印亭(John Poynting)
- 提出時間:1884年
- 適用領域範圍:電磁波與微波技術
定理公式
積分形式的坡印廷定理


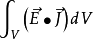

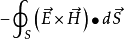
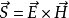

微分形式的坡印廷定理

推導過程
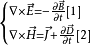
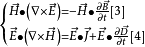
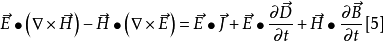
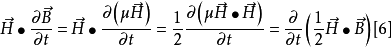
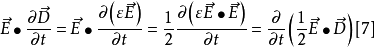
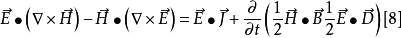



定理影響



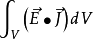

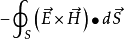
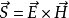


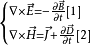
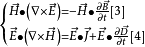
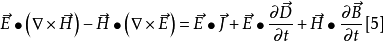
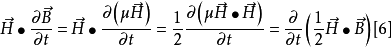
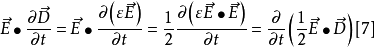
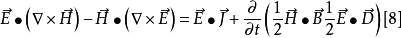




坡印亭定理,英文表示Poynting theorem,是1884年約翰·坡印亭(John Poynting)提出的關於電磁場能量守恆的定理。他認為電磁場中的電場強度E與磁場強度H叉乘所得的矢量...
坡印廷定理,英文表示Poynting theorem,是1884年約翰·坡印亭(John Poynting)提出的關於電磁場能量守恆的定理。他認為電磁場中的電場強度E與磁場強度H叉乘所得的矢量...
波印亭定理是約翰·亨利·波印亭發現的關於電磁場的能量守恆的定理。它把能量密度u的時間導數,與能量的流動,以及與電磁場做功的速率聯繫起來。由以下的公式總結: ...
5.3 坡印亭定理與坡印亭矢量5.3.1 時變電磁場的坡印亭定理與坡印亭矢量5.3.2 時諧電磁場的坡印亭定理與復坡印亭矢量5.4 電基本振子和磁基本振子5.4.1...
5.4 坡印亭定理和坡印亭矢量5.4.1 坡印亭定理5.4.2 坡印亭矢量5.5 波動方程5.5.1 無源導電介質中的齊次波動方程5.5.2 無源理想介質中的齊次波動方程...
1.3線性各向異性介質的坡印亭定理 1.4非線性介質的坡印亭定理 1.5電路集中化假設 1.6小結 參考資料 第二章線性直流網路 2.1直流網路中的兩個守恆定律 2.2由第...
坡印亭矢量(英語:Poynting vector),亦稱能流密度矢量,其方向為電磁能傳遞方向,大小為能流密度(單位面積的能量傳輸速率)。坡印亭矢量的SI單位是瓦特每平方米(W/m...
關鍵字:光 電磁波本質 邊界條件 反射定律 折射定律 坡印亭定理 能量守恆定律 學科分類:O431.1[數理科學和化學 > 物理學 > 光學 > 光本性的理論 > 光的電...
3.3.4頻域坡印亭定理 3.4電磁場的格林張量 3.4.1頻域格林張量 3.4.2時域格林張量 3.5互易關係 3.5.1洛倫茲定理 3.5.2格林張量互易關係和電磁場 3.5.3電磁...
例如,在求天線的輸入阻抗時,先假設其上的電流分布為正弦分布,據此並利用坡印亭定理求出由天線表面發出去的功率除以最大電流的平方(半波振子)而得到輸入阻抗。這種...
§6-2 坡印亭定理與坡印亭矢量§6-3 動態位§6-4 達朗貝爾方程的解答§6-5 輻射§6-6 電介質中的平面電磁波·波的極化§6-7 平面波的反射與折射·介質...
5.7.1坡印亭定理5.7.2 坡印亭矢量5.8 正弦電磁場5.9 工程套用實例5.10 本章 小結5.11 習題5.12科技前沿第6章 準靜態電磁場...
3.坡印亭定理和坡印亭矢量4.時諧變場量的複數表示法5.波動方程6.標量位和矢量位二、重點、難點及其分析1.有關麥克斯韋方程組的幾個問題2.有關電流的概念...
2.1.3坡印亭定理22 2.1.4渦電流23 2.2穩態強磁場基本理論24 2.2.1洛倫茲力24 2.2.2磁化力25 2.2.3磁力矩27 2.2.4磁化能27 2.2.5磁極間相互...
第六節 坡印亭定理及坡印亭矢量第七節 動態位第八節 波動方程第九節 電磁場與電路的關係小結習題第五章 平面電磁波第一節 理想介質中的均勻平面波...
