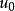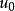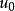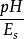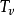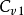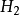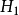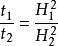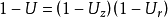土體固結理論

土體在外加荷載作用下，由於孔隙比減少而壓密變形，同時提高了強度。對於飽和土，只有當孔隙水擠出以後，變形才能產生。開始時，土中應力全部由孔隙水承擔。隨著孔隙水的擠出，孔隙水壓力逐步轉變為由土骨架承受的有效應力。研究這兩種應力的相互消長以及土體變形達到最終值的過程，稱為固結理論。

基本介紹

• 中文名：土體固結理論
• 外文名：consolidation theory of soil
• 對象：土體
• 類別：理論
• 作用方式：外加荷載作用
• 學科：土木工程

土體固結理論介紹

砂性土的變形在外加荷載施加以後很快完成，而粘性土由於透水性低，其變形的發展在外加荷載作用以後還要延滯很長時間。因此，研究固結是針對粘性土，而且首先針對飽和粘性土。
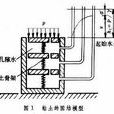
為了說明粘土的上述應力變化過程而提出了固結模型(圖 1)。它由若干帶有小孔的活塞用彈簧串聯而成，並放 在注滿水的容器中。彈簧和水分別表示土骨架和孔隙水，小孔的大小則象徵土透水性的高低。當外加荷載未施加時，土中只有靜水壓力；施加荷載以後，就增加了相當於p的超靜水壓力 。此時，水還來不及從小孔中排出，彈簧沒有壓縮，說明外加荷載p全部由水承擔。隨著時間的推移，不同深處的水以不同的流速v向外排出，各個彈簧產生不同程度的壓縮，這表示超靜水壓力部分地轉移到土骨架上，從而使有效應力σ′逐步增長。從容器壁上接出的測壓管可以觀測不同深度的孔隙水壓力隨時間的變化。最後，彈簧的壓縮趨於穩定，水壓力也減小到原來的靜水壓力，亦即外加荷載全部由彈簧承擔，固結過程因而結束。在任何時刻，σ′與u之和恆等於該點的總應力σ(見土體的壓縮和變形)。

主固結

考慮位於不透水層上面、厚度為H的飽和粘土層，其頂面為透水砂層,地下水位與粘土層頂面相平(圖2a)。當時間t=0時，在外加荷載p作用下，土中不同深度的初始孔隙水壓力 處處為p，其後孔隙水逐步由砂層排出，它的滲流服從達西定律。接近頂面的水最易排出，所以這裡的滲透速度v最大。隨著時間的推移(0< < )，粘土層逐步固結，v值也越來越小。同時，孔隙水壓力u也逐步轉移為有效應力σ′。兩者既是深度z也是時間t的函式，但其和恆等於外加荷載。孔隙水的排出與土骨架的壓縮是耦合的，但在不同時間和不同深度，粘土層的單位壓縮量ε也是不同的。當 全部轉移為σ′時，土層的最終壓縮量S∞為 （ 為粘土層的壓縮模量），主固結過程完成。

在工程實踐中，當粘土層中的孔隙水沿坐標系的三個方向滲流（如高層房屋的地基）時，應採用三維固結理論。二維固結理論則用來研究孔隙水主要沿兩個方向滲流（如土壩及其地基）的情況。但當受荷載面積遠大於粘土層厚度時，孔隙水主要沿豎直方向滲流，可近似地用一維固結理論研究孔隙水壓力的變化過程。

次固結

將室內固結試驗結果繪製在壓縮量-時間對數曲線上，可以發現在主固結（圖3中的ab段）達到98%(相應的時間為 )以後，變形仍在發生，這部分稱為次固結（圖3）中的bс段。次固結是在有效應力基本上不變的情況下發生的，並與土層厚度無關。它的產生歸因於土骨架的蠕變和土中結合水與土骨架之間相互作用的鬆弛，因此，達西定律不再有效。對於塑性指數很高的軟粘土和有機質土，次固結常占可觀的百分比。

一維固結

當孔隙水主要沿豎直方向滲流時，K.泰爾扎吉（一譯太沙基）根據飽和土中微分單元在單位時間內的流量變化與孔隙比變化率相等的條件，建立了孔隙水壓力u和深度z、時間t的一維固結微分方程

(1)

(2)

式中 為固結係數（ ）；K為豎向滲透係數；e為孔隙比；a為壓縮係數； 為水的容重。式(1)表示孔隙水壓力u的消散速率與土的滲透係數K和土的壓縮模量 =(1+e)/a成正比。隨著粘土層的逐步固結，K值減小而 值增大，但兩者的乘積，即 卻大致保持不變。根據問題的起始條件和邊界條件，可以用傅立葉級數表述固結方程(1)的解u。
將任一時刻土層中的有效應力面積對於總應力面積之比，亦即已經完成的固結變形 對於固結終了時的總變形S∞之比稱為固結度U。固結度U與時間因素 之間存在著單值關係，在工程設計中用來計算完成一定固結度所需的時間或在指定的時間已經完成的沉降值 。
在固結計算中，重要的是如何測定固結係數 。它經常用室內固結試驗測定。由於土的應力狀態和結構在鑽探取樣過程中發生改變和受到擾動，所以假使有兩個土質相同( = )、但厚度不等( > )的土層，在達到相同固結度時的時間因數必然相等，即

或 (3)

式(3)表示完成同一固結度所需的時間與最大滲徑H的平方成正比。因此，可以根據固結試驗的成果來估計實際土層完成同一固結度所需的時間。
在沉積過程中，由於較多的顆粒呈水平向排列，並間或夾有薄層粉砂，致使孔隙水的滲徑大大減小。所以建築物地基的實際固結過程要比理論計算結果快一些。

三維固結

M.A.畢奧於1941年提出了三維固結理論，也稱畢奧理論。他考慮了各向同性的飽和土單元體在外力作用下的平衡條件，土骨架的線性變形和孔隙水滲流的連續性條件。其優點是不但可以求出孔隙水壓力隨時間的變化，而且還可以計算相應的土體變形。由於它的精確解相當複雜，只有在少數情況下才能得到解析解。目前，由於電子計算機和有限元法的發展，畢奧理論才得到較廣泛的套用。
在實際工程中，常在軟粘土中設定砂井(見預壓法)，依靠豎向和徑向滲流加速地基排水固結。如果求得某一時刻由於豎向滲流而引起的固結度為Uz，而同一時刻由於輻射向滲流所引起的固結度為Ur，則地基的總固結度U可以從下式求出：

R.A.巴倫於1948年提出了完整的砂井設計理論，成為目前一種加固軟土地基的有效方法。

太沙基固結理論

太沙基在1924年建立了一個一維固結模型和建立了一維固結理論。太沙基一維固結理論為求飽和土層在滲透固結過程中任意時間的變形，通常採用太沙基提出的一維固結理論進行計算。太沙基固結理論採用的物理模型的基本假設如下：

（1）土體是飽和的；

（2）土體是均質的；

（3）土顆粒和孔隙水在固結過程中都是不可壓縮的；

（4）土中水的滲流服從於達西定律；

（5）在固結過程中，土的滲透係數k是常數；

（6）在固結過程中，土的壓縮係數a是常數；

（7）外部荷載是一次瞬時施加的；

（8）土體的固結都是小變形；

（9）土中水的滲流與土體變形只發生在一個方向。

土中附加應力沿水平面是無限均勻分布的，因此土層的壓縮和土中水的滲流都是一維的；在這些假設的基礎上，太沙基建立了一維固結理論。許多的心的固結理論是在減少這些假設條件的基礎上發展起來的。所以說太沙基一維固結理論是最基礎有意義的固結理論。

研究表明，對於均值地基，即使附加應力隨深度變化，但不同深度的同一水平面上的附加應力相同，則該水平面各個點的壓縮變形相同，且符合側限變性條件。當壓縮模量或壓縮係數不變時，對於任一隨深度變化的附加應力作用下，其單向固結變形可以套用疊加原理，相當於壓縮應力圖形中各部分在同一時刻引起變形的代數和。

自太沙基一維固結理論提出的半個多世紀以來，人們已有大量的工程實踐和改進方法，但是問題仍然沒有完全解決。在實際工作中常常發現太沙基一維固結理論計算的沉降速率遠小於實測值。為此，設計人員常常感到困惑，選用勘探取樣室內試驗結果得到的壓縮性指標，進而求得固結計算結果到底有多大的把握。