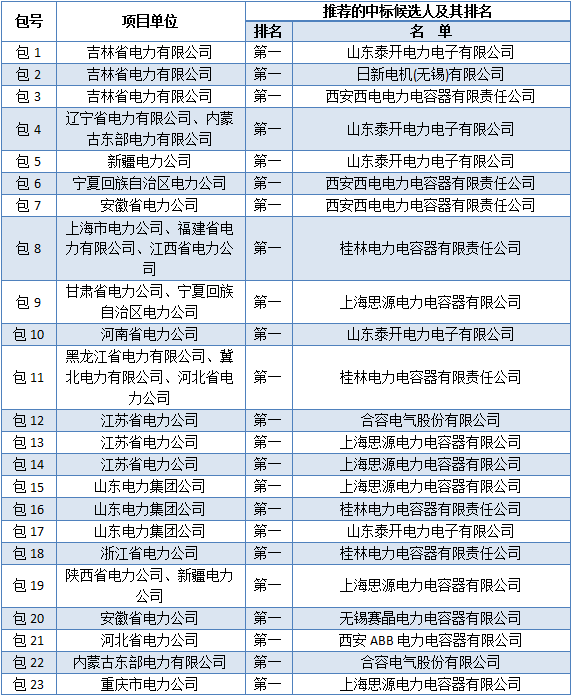
國家電網電容器投標報價模型對於投標企業來說投標報價策略與決策事關企業的興衰與生死存亡,一個合理的投標報價模型是提高投標中標率的關鍵,決定著企業經濟效益並影響著企業未來的發展。 如何依據招標單位的評標方法,在分析競爭對手過去已有的報價數據基礎上構建有效的投標報價模型,並以此為依據制定出既有最優利潤又有較高中標率的合理報價,成為投標企業生死攸關的大事。
國家電網電容器投標報價模型和理論主要有:(1)在綜合評標法的基礎上,以數理統計原理和模糊數學綜合評判理論為依據的工程投標最優報價的報價策略模型。(2)利用數理統計的回歸分析理論,確定其報價函式以及優勢報價區間的報價模型。(3)基於貝葉斯博弈均衡理論,針對合理低價評標法,從雙方博弈和多方博弈兩個角度建立的最最佳化投標報價模型。
基本介紹
- 中文名:國家電網電容器投標報價模型
- 外文名:A Price-Bidding Model for National Grid Capacitors
- 作用:提高投標中標率
- 對象:投標企業
- 行業:國家電網
- 投標難點:大型、複雜、招投標行為多批次
簡介,具體模型,區間平均下浮雙邊曲線算法,非合作模式下浮比例可變投標報價模型,馬爾科夫分析法計算各類貨物平均,總結與建議,
簡介
隨著國家的基礎設施建設進一步擴大,國家電網建設所用的電容器採購方式採用招標投標形式,招標投標在國家及企業建設的物資採購中套用越來越廣。隨著招標投標所面對的經濟對象不斷大型化、複雜化和招投標行為的多批次化,給投標商帶來新的挑戰。
根據國家電網電容器投標計畫,國家電網於2013—2015年每年舉行6批電容器類貨物的招標。每批又分若干包,不同包包含的電容器規格、數量不同。依據以往數據顯示,參加投標廠家每年基本固定。主要廠家有17家。國家電網在2013—2014年採用的是綜合評標法進行招標。該評標辦法中,技術、價格、商務占的比例分別為30%,60%,10%。以總分100分計。假定各廠家在技術、商務方面實力基本相當,因此此問題中各廠家只需考慮通過合理的投標報價提高價格得分,得到價格得分第一就認為中標。各投標廠家具體得分情況以區間平均下浮雙邊曲線算法計算。
國家電網電容器投標報價模型主要有:區間平均下浮雙邊曲線算法、非合作模式下浮比例可變投標報價模型、馬爾科夫分析法計算各類貨物平均。
具體模型
區間平均下浮雙邊曲線算法
1 計算原則
對於某批次某包中基準價的計算區間,以該包中各廠家全部有效投標報價算術平均值A的80%—115%為基準區間,根據不同批次各包投標報價的不同情況可分為以下3種情況,其中以A1作為有效報價的算術平均值。
1) 若在某一批次的某一個包中的投標報價全部在基準區間內,則A1表示該包全部投標報價的算術平均值,以B作為基準價,則B=A1*(1-a),其中a為下浮比例(或稱下浮係數、價格下浮基準點);
2) 若在某一批次的某一個包中的投標報價既有在基準區間內的也有在區間外的情況,則先剔除區間外的報價,以全部基準區間內的有效投標報價算術平均值作為A1,計算基準價B=A1*(1-a);
3) 若在某一批次的某一個包中的投標報價都在此區間外,則所有基準區間外的投標報價即為有效投標報價,計算算術平均值A1,基淮價B=A1*(1-a);
2 區間平均下浮雙邊曲線算法的價格得分
求所有參與投標報價廠家出價的算數平均數A,設某種配備貨物有N個公司參加報價,報價分別為xi(i=1,2,…,N)。
求算數平均數A1。A1表示所有參與投標報價廠家的出價中落在有效基準區間內的價格的算術平均值。設參加該種配備貨物報價的N個公司有M個公司的報價均落入(0.8A,1.15A)有效基準區間(即0<M<N),其有效報價為x′i(i=1,2,…,M),則
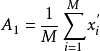
當M=N時(即參加該種配備貨物報價的N個公司全部落入(0.8A,1.15A)有效基準區間內時),有A1=A,基準價B=A1×(1-a);
當M=0時(即參加該種配備的貨物報價的N個公司全部落入有效區間(0.8A,1.15A)外時,有A1=A,基準價B=A1×(1-a)。
價格得分計算公式為:
當P≥B,得分DF=(B/P)n;
當P<B,得分DF=(P/B)m。
式中:P為投標人的評標總價;m,n為減分速率指數。
本例中n,m取值有2種情況:n=1.5,m=0.6;n=2.0,m=0.3。
非合作模式下浮比例可變投標報價模型
1 計算方法
在非合作模式下浮比例可變投標報價模型中,假設第i批中某種配置的貨物所有投標報價的廠家共ni個,另設需要幫助設計投標的廠家(以下用甲廠家表示)原報價為xi,ni,其餘ni-1個廠家報價分別為xi,1,xi,2,…,xi,ni-1,故在基本假設中假設所有報價均在有效報價區間,以此為例計算基準價為
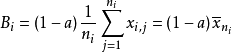
式中:xi為各廠家在第i批貨物某包的投標報價的算術平均值;
Bi為第i批中某種配置的貨物所有投標報價的基準價。
設Ai為第i批中某包配置的貨物投標報價的算術平均值,為使甲廠家價格報價得分最高,設甲廠家投標報價為Hi,則Hi為最優報價,有
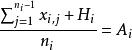
若全部報價均落在有效報價區間,以A1i表示第i批貨物某包的有效投標報價算術平均值,則A1i=Ai,相應的該批貨物基準價Bi′為Bi′=A1i(1-a),式中Bi′為理想基準價,即甲廠家在最優報價時所得到的基準價。由價格計算得分公式分析可知,報價越接近基準價,得分越高,因此最優報價為Hi=Bi′,根據分析,有:
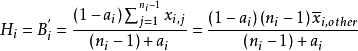
式中xi,other為除甲廠家外其餘的ni-1 廠家對第i 批該配置貨物報價的平均值。
2 定量分析的方法與步驟
分析甲廠家歷年來的投標報價資料,用數理統計的方法,統計計算報價水平與投標成功率的關係,繪製報價與中標率的散點分布圖,然後利用數學回歸擬合的方法,分析得出報價水平與中標率的相關關係數學公式,以此為投標報價決策提供理論依據。
首先,計算出投標單位j在歷次投標中所有報價的平均值,為(A1j,A2j,…,Anj),則Nij=Bij/Aij。其中Nij為投標單位j在第i次投標中的標準標價比值,Aij為投標單位j在i次投標報價的平均值;Bij為投標單位j在第i次投標的報價。
然後計算投標單位j在各次投標中標準價比值的平均值,也為平均標價比值。
馬爾科夫分析法計算各類貨物平均
馬爾科夫分析法認為某一系統在現在情況已知的情況下,系統未來時刻的情況只與現在的狀況有關,與過去的歷史無直接關係。而該項目的報價也存在以下特點:
1)配置相同的包(貨物類型相同,數量相同、下浮比例也相同的包)在不同投標批次中報價不同;
2)下一批次合包的報價受到當前批次的報價情況的影響,即2014年第4批各包報價受2013年第3批各包報價的影響。故2014年第4批各包的每類貨物的報價由2013年第3批各包的每類貨物的平均報價所決定。
設狀態機率πj(k)表示的是事件在歷史狀態為已知的條件下,經過k次狀態轉移後,第k個批次處於的狀態Ej的狀態機率。從初始狀態開始,經過k次狀態變換後達到狀態Ej的這一狀態轉移過程,pij為在轉移過程的條件機率,根據馬爾科夫過程的無效性及條件機率公式有:
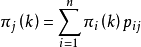
若行向量為π(k)=[π1(k),π2(k),…,πn(k)],再由式
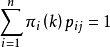
可得到以下的公式
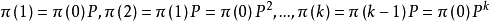
總結與建議
在模型分析的基礎上對國家電網招投標方法的改革提出如下建議:
1)通過對國家電網綜合評標法評標的價格得分算法分析,國家招投標方法改革應趨向於降低國家電網建設的投資。國家電網可以通過對下浮比例的增加來降低各個投標廠家的整體價格得分,從而減少國家電網的建設成本;
2)通過降低減分速率指數m,同時增加減分速率指數n,來驅使投標商降低投標報價來獲得較高的報價得分,從而使區間平均下浮雙邊曲線算法計算的基準價降低,使國家電網低價購得同樣數量與質量的電容器;
3)綜合評標法中的區間平均下浮雙邊曲線算法的區間範圍可適當減小。