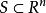設X和Y是拓撲空間，f:X→Y是映射。若對於Y中任意的緊集C，f-1(C)是X中的緊集，則稱映射f是固有的。
基本介紹
- 中文名：固有映射
- 外文名：proper mapping
- 適用範圍：數理科學
簡介,判定,度量空間,巴拿赫空間,緊集,
簡介
固有映射是指緊集的原像是緊集的映射。
設X和Y是拓撲空間，f:X→Y是映射。若對於Y中任意的緊集C，f-1(C)是X中的緊集，則稱映射f是固有的。
判定
度量空間
當X和Y為度量空間時，映射f:X→Y為固有映射的充分必要條件是：f是閉映射（映閉集為閉集）且Y中每點的原像是X中的緊集。
巴拿赫空間
當X和Y是巴拿赫空間時，連續線性運算元A:X→Y為固有映射的充分必要條件是：A為單射且A的像空間ImA是閉的。
賦范線性空間中閉集上的緊連續場，特別地有界閉集上的全連續場，是固有的。
設X和Y是道路連通的度量空間，f:X→Y是局部同胚，那么f是固有映射=f是閉映射⇔f是有限層覆蓋映射。
緊集
如果一個集合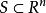
包含在某個球內，也即存在
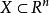和
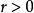使得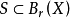
，那么該集合是有界的(bounded)。
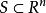
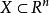
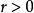
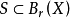
有界的定義可以用某個固定的球心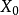
表述，因為如果一個集合包含在球
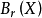中，那么它也包含在球
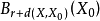中。我們通常設定
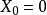來討論有界性。
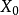
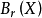
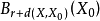
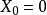
如果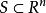是有界的閉集，那么S是緊集。
