回溯集(retraceable set)是一種回歸集。德克爾(Dekker,J.)和邁希爾(Myhill,J.)證明了:若A為遞歸集,則A為回溯集。反之,若A為回溯集,則A必為遞歸或禁集。另外,曼斯費爾德(Mansfield,R.)證明了:若A,A-都是回溯集,則A一定是遞歸集。
基本介紹
- 中文名:回溯集
- 外文名:retraceable set
- 領域:數學
- 學科:集合論
- 性質:回歸集
- 重要人物:德克爾、邁希爾
概念,遞歸可枚舉集,回歸集,遞歸函式,自然數集,
概念
回溯集(retraceable set)是一種回歸集。設A為自然數集,a0<a1<a2…為A依自然大小次序給出的枚舉。若存在部分遞歸函式φ,使A關於這種枚舉由φ回歸的,即:
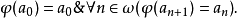
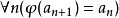
遞歸可枚舉集
亦稱半遞歸集。簡稱re集。一種自然數集合。設A為一個自然數集合,若存在一個能行過程把A的所有元素能行地列舉出來,則稱A為遞歸可枚舉的。等價地,A為re集,若且唯若A=∅,或存在遞歸函式f,使A=rang (f)。在後一種情形,f稱為A的枚舉函式。若A是re集,則對n∈A,總可以在有限步內能行地判定。因為只要用A的枚舉函式f能行地枚舉出f(0),f(1),f(2),…,必定會有某個m,使f(m)=n。從這個意義上說,re集只具有半可判定性。但是,當A的余集A-也是re集時,A一定是遞歸的。從而是全可判定的。另一方面,因為A為遞歸集,若且唯若A和A-都是re集。所以,遞歸集都是re集。
re集是能行性理論的基本概念之一。設A是自然數集的一個子集,如果存在一個遞歸函式f(x)使得A是f(x)的值域或A是空集,就稱A是遞歸可枚舉集。換言之,當A是非空的遞歸可枚舉集時,A中的元素可以通過遞歸函式f一個一個地枚舉出來,使得f(0),f(1),f(2),……成為A中一切元素的一個序列,這裡需要注意的是這個序列中的對象可能有重複,另外f(x)也不一定是單調函式。遞歸可枚舉集有多種彼此等價的定義方法。設A是自然數集的一個子集,則下列條件等價:
(1) A是遞歸可枚舉集;
(2) A是某一個部分遞歸函式的值域;
(3) A是某一個部分遞歸函式的定義域;
(4) A的部分特徵函式是部分遞歸函式;
(5) A是某一個原始遞歸函式的值域;
(6) A是空集或某一個遞歸函式的值域。
對於n元自然數組集合A,即A⊆N(N是自然數集),也可類似地定義遞歸可枚舉性。用遞歸可枚舉性可定義遞歸性:集合A是遞歸集合若且唯若A及Ᾱ(A的余集)皆為遞歸可枚舉集。遞歸集都是遞歸可枚舉的,但是反之不然,存在某些遞歸可枚舉集並不是遞歸集。
回歸集
回歸集是re集的一種推廣。設A為自然數集合,A={a0,a1,a2,…}為A的一種無重複枚舉。若存在部分遞歸函式φ,使得φ(a0)=a0& ᗄn∈ω(φ(an+1)=an),則稱A為關於這種枚舉的由φ回歸的集合,並稱φ為A的回歸函式。若存在A的一種無重複枚舉和一個部分遞歸函式φ,使得A為關於該枚舉由φ回歸的,則稱A為回歸集。德克爾(Dekker,J.)和邁希爾(Myhill,J.)證明了:若A為re集,則A一定是回歸集。反之,若A是回歸集,則A必定是re集或禁集。另外,阿佩爾(Appel,K.I.)和馬克勞林(Mclaughlin,T.G.)證明了:若A,A-都是回歸集,則A和A-中至少有一個是re集。
注意到若A是re集,則一定存在一種(能行的)無重複枚舉A={a0,a1,a2,…},並且總存在部分遞歸函式φ,使ᗄn∈ω(φ(an)=an+1)。集合的回歸性是由遞歸可枚舉性導出的一個概念。
遞歸函式
函式的概念是一個很一般的概念。在定義函式時,不一定要具體給出通過自變數求函式值的方法。因此,可將函式分成兩類,一類是所謂能行可計算函式,另一類是非能行可計算的函式。這前一種函式無論在理論上或在實際上都是非常重要的,因此人們便試圖給它們以精確的數學刻畫。遞歸函式便是許多這種刻畫中的一種。
我們以下考慮的函式都是從自然數到自然數的函式。
我們先定義幾個初等函式:
(1)零函式 Z(x)=0;
(2)後繼函式 S(x)=x+1;
(3)廣義麼函式 U1n(x1,…xn)=xi;
顯然,上面這些函式都是能行可計算的。
再介紹幾個將函式變換為函式的運算元。
(1)複合運算元 設f是n元函式,g1,…,gn是m元函式,複合運算元將f,g1…gn變換成為如下的m元函式h:
h(x1,…,xm)=f1g1(x1,…xm),…gn(x1,…xm))
(2)遞歸運算元 設f是n元函式 (≥0),g是n+2元函式,遞歸運算元將f,g變換成滿足下列條件的h+1元函式h:
h(x1,…,xn,0)=f(x1,…,xn);h(x1,…xn,y+1)=g(x1,…xn,y,h(x1,…,xn))
(3)μ一運算元,設f是n+1元函式,如果存在y,使f(x1,…,xn,y)=0,我們以μyf(x1,…,xn,y)表示這樣的y中的最小者,如果使f(x1,…,xn,y)=0的y不存在,我們說μyf(x1,…,xn,y)無定義。μ-運算元將n+1元函式f變換成下面的幾元函式h
h(x1,…,xn)=μyf(x1,…,xn,y)
注意,μ運算元可以將一個全函式變換成一個部分函式(即在自然數的某個子集上有定義的函式)。
可以看出,上述所有運算元都是將能行可計算函式變換為能行可計算函式。
所謂遞歸函式類便是包含零函式、廣義麼函式,並在複合運算元、遞歸運算元,μ-運算元下封閒的最小函式類。
容易相信,任何遞歸函式都是能行可計算的。反過來,是否存在直觀上能行可計算的,但不是遞歸的函式呢?人們直到現在還沒有發現這樣的函式。相反,人們證明了,現已遇到的直觀上能行可計算的函式都是遞歸函式。進一步,人們還證明了,遞歸函式類與其他的一些刻畫能行可計算函式的方法產生的函式類是完全一致的,這些事實促使車爾赤(Church)提出了他的著名的論點:
遞歸函式類與直觀能行可計算函式類是重合的。
這個論點已被大多數遞歸論學者所接受。
自然數集
一種特定的集合。指全體自然數的集合。常用符號N表示。自然數集有如下性質:
1.在自然數集N中,有一個最小的自然數0;在N中除去0之後,其餘的自然數構成的數集稱為正整數集,常用符號N+(或N)表示,1在N+中是最小的元素;在N和N+中都沒有最大的自然數;它們都是無限集。
2.自然數1通常稱為單位。
3.在N或N+中,任取一數在它上面加單位1,所得的數稱為該數的後繼數。從最小元素開始逐個加1,這樣無限地進行下去,就可得到該數集中所有其他元素,最小元素不是任何元素的後繼數。
4.1可整除任何自然數,其商仍為原自然數,所以1是任何自然數的約數。
5.0加任何自然數,其和仍是原來那個自然數,1乘任何自然數,其積仍是原來那個自然數,所以自然數都是1的倍數。
7.如果0具有性質P,則任何具有性質P的自然數的後繼數都具有性質P(此即歸納原則,是完全歸納法的原理)。
8.在自然數集N中的數,可以按順序一個一個地數下去,所以自然數集是可數集。
9.在自然數集N中的任意兩個元素都可以比較大小,所以自然數集是有序集。
10.在自然數集N中,加法與乘法兩種運算,總可以實施,即自然數的和與積仍是自然數。
11.在自然數集N中的加法、乘法運算滿足交換律、結合律和乘法對加法的分配律。
12.在自然數集N中的加法、乘法運算滿足消去律:
m+k=n+km=n (m,n,k∈N),m·k=n·km=n (m,n∈N;k∈N+)。
13.自然數集的任一非空子集必存在一個最小的自然數,此結論稱為最小數原理。
