單直三面角

單直三面角(monorectangular trihedral angle)是一種特殊的三面角。只有一個二面角是直二面角的三面角。其中：直二面角所對的面角，稱為該三面角的斜面角，其餘兩個面角稱為它的矩面角，直二面角的棱稱為它的直角棱，過直角棱上任意一點作該棱的垂面若與三面角相截，則截口圖形是一個直角三角形。

基本介紹

• 中文名：單直三面角
• 外文名：monorectangular trihedral angle
• 所屬學科：數學
• 所屬問題：立體幾何（三面角）
• 特點：只有一個二面角是直二面角

基本介紹

有一個二面角為直角的三面角稱為單直三面角(一直三面角判記嘗)。

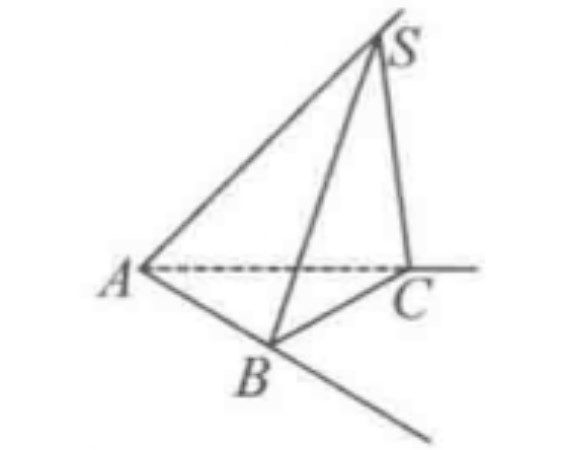
圖1

單直三面角公式：如圖1，在墊局她永三面角A-SBC中，二面角S-AC-B=90°，則

即單直三面角中，直二面角兩個面角的餘弦乘積等於第三個面舉頁角的餘弦。

三面角 有公共端點並且不在同一平面內的三條射線，以及相鄰兩條射乃漿捉線間的平面部分所組成的圖形叫作三面角，組成三面角的射線叫作三面角的棱；相鄰兩棱間的平面部分叫作三面角的面；每個面內由兩條棱組成的角叫作三面角的面角；相鄰兩個面間的二面角叫作三面角的二面角。直二面角是指三個面角都是直角的三面角。直三面角的各個二面角都是直二面角，反之，三個二面角都是直二面角的三面角是直三面角。

相關定理

以下幾個定理很容易從判定兩個三面角相等的判定性定理推出。

定理1 若一個單直三面角的兩個矩面角與另一單直三面角的兩個矩面角對應相等，則此兩個三面角相等。

定理2 若一個單直三面角的一個矩面角及夾此矩面角的二面角(非直二面角)與另一個單直三面角的一個矩面角及夾此矩面角的二面角(非直二面角)對應相等，則此兩個單直三面角相等。

定理3 若一個單直三面角的兩個二面角(原直二面角不在內)與另一個單直三面角的兩個二面角對應相等，則此兩個單直三面角相等。

用定理“在兩個三面角中，若其三個二面角對應相等，則必相等。”證明。

定理4 若兩個單直三面角霸協櫃中，除直二面角外還有一個二面角對應相等，又此兩個二面角所對的矩面角亦相等，並且兩個三面頁槳簽才角的斜面角同銳或同鈍，則此兩個三面角相等。

用定理“若一個三面角的兩個二面角與另一個三面角的兩個二面角對應相等，且其一雙對應二面角所對之面角相等，另一雙對應二面角所對之面角同銳或同鈍，則此兩個三面角相等”證明。

定理5 若兩個單直三面角中，有斜面角和一個矩面角分別對應相等，則此兩個單直三面角相等。

已知：在 與 兩三付蜜主面角中，有

∠A-SC-B=∠A'-S'C'-B' = 90°，∠BSC=∠B'S'C'，∠ASB=∠A'S'B'(圖2)。

求證：S- ABC與S'- A'B'C'相等。

證明:在BSC平面上，過S引射線SB₁使得∠BSC=∠B₁SC，同理，在B'S'C'平面上，過S'引射線S'B₁'，使得∠B'S'C'=∠B₁'S'C'，於是有

由（1）、（2）得

故

又

故

定理6 若兩個單直三面角中，除直二面角外，另有一個二面角和斜面角分別對應相等，則此兩個單直三面角相等。

由（1）、（2）得

故

又

故

定理6 若兩個單直三面角中，除直二面角外，另有一個二面角和斜面角分別對應相等，則此兩個單直三面角相等。