商對象(quotient object)是商代數系概念的推廣。它是子對象的對偶概念。設A,B為範疇C的兩個對象。若有滿態射π:A→B,則稱B為A的商對象。
基本介紹
- 中文名:商對象
- 外文名:quotient object
- 領域:數學
- 學科:範疇論
- 性質:商代數系概念的推廣
- 對偶:子對象
概念
商範疇

範疇
同態
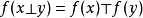
商對象(quotient object)是商代數系概念的推廣。它是子對象的對偶概念。設A,B為範疇C的兩個對象。若有滿態射π:A→B,則稱B為A的商對象。

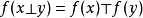
數據挖掘DM經過確定業務對象、數據準備、建立模型、驗證模型、數據挖掘、結果分析等步驟,不僅完成了對歷史數據的分析,以及不同客戶群體的消費數據的分析,而且將這些...
運算元據層中保存的是可以被數據分析處理算法直接套用的數據對象。數據源層中的數據是原始數據,在存儲格式、數據表結構等方面不相同,同時也存在著較多的髒數據,必須...
本書以大數據為背景,以商務經濟管理活動中的問題為對象,綜合運用統計學、套用數學、管理科學(運籌學)、計算機軟體套用和編程、數據挖掘、機器學習等學科知識,對商務...
中國商業數據中心利用自身的企業調查能力和廣泛的信息渠道來源,幫助客戶發掘最有成長力的公司和最合適的投資併購對象,降低併購前雙方的信息不對稱性和併購風險。 從多...
2.3 Access2003基本對象簡介(15)2.4 獲取幫助(20)實訓構造庫房管理系統(22)思考與練習(28)項目三 創建資料庫和表(29)3.1 創建“庫存管理”資料庫(29)...
而對外合作指標則根據具體合作對象而定,譬如某電商網站與返利網合作,首先考慮的也是合作回報率。電子商務數據分析客戶價值指標 一個客戶的價值通常由三部分組成:歷史...
主要內容包括:資料庫系統概述、關係資料庫、關係資料庫標準語言(SQL)、查詢最佳化、關係規範化理論、面向對象與UML基礎、資料庫設計、資料庫管理;簡要介紹了資料庫技術...
3.2.3 對象之間的相似性度量 373.3 k-means 算法及其改進 393.3.1 k-means 算法 393.3.2 k-means聚類算法的改進 413.4 一趟聚類算法 463.4.1 ...
把握交易對象的結算時期與喜好的分析 專欄 統計學分析方法是一種人工智慧 156 第6 章 商品開發的統計學 .157 6.1 | 預測新商品的銷售走向 158 通過統計提前掌...
主要內容包括:資料庫系統概述、關係資料庫、關係資料庫標準語言(SQL)、查詢最佳化、關係規範化理論、面向對象與UML基礎、資料庫設計、資料庫管理;簡要介紹了資料庫技術...
