哥德爾配數

Gedeer Peishu 哥德爾配數使用素數冪 的乘積來表示自然數的任意有限序列xo，x1，…，xn 的所有方案。表示本身稱為序列x。，xl，…，x，的 哥德爾數，通常記為（x。，x，，…，x。）。

基本介紹

• 中文名：哥德爾配數
• 外文名：Gedeer Peishu
• 使用：素數冪 的乘積
• 表示：自然數的任意有限序列
• 學科：數理科學
• 縮寫：GN

簡介

在形式數論中，哥德爾編號是對某些形式語言的每個符號和公式指派一個叫做哥德爾數(GN)的唯一的自然數的函式。這個概念是哥德爾為證明他的哥德爾不完備定理而引入的。

可計算函式集合的編號有時叫做哥德爾編號或有效編號。哥德爾編號可以被解釋為一個程式語言，帶有指派哥德爾數到每個可計算函式作為在這種程式語言中計算這個函式的值的程式。Roger 等價定理特徵化了是哥德爾編號的可計算函式集合的編號。

哥德爾編碼

哥德爾使用基於素數因數分解的哥德爾編碼系統。他首先把唯一的自然數指派到在他所處理的算術的形式語言中的每個基本符號。

為了編碼是符號序列的整個公式，哥德爾使用了如下系統。給出正整數的序列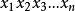 ，哥德爾對這個序列的編碼是第n個素數自乘這個序列中對應值的次數：

依據算術基本定理，用這種方式獲得的任何數都可以唯一的因數分解到素因子，所以可以有效的從其哥德爾數恢復最初的序列。

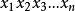
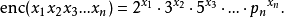
哥德爾特別的在兩個級別使用這個方案： 首先編碼表示公式的序列，其次編碼表示證明的序列。這允許他證明在關於自然數的命題和關於自然數的定理的可證明性的命題之間的對應，這個證明的關鍵觀察。

有更複雜的（但更“簡潔”）的方式來構造序列的哥德爾數。

唯一性的缺乏

哥德爾編號不是唯一的。一般性的想法是把公式映射自然數上。假設有K個基本符號。可替代的哥德爾編碼可以通過把每個基本符號映射到基數為K的記數系統的一個數字來構造，這樣由n個符號的字母串構成的公式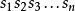 將被映射成數

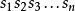
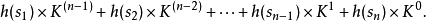
換句話說，藉由將K個基本符號以某種固定順序擺放，那么每個方程式就會產生唯一對應的哥德爾數。但是如果將K個基本符號以另一種固定順序擺放，則會產生另一種哥德爾編號。

形式系統套用

還有，哥德爾編號蘊涵了形式系統的每個推論規則都可以被表達為自然數的函式。如果f是哥德爾映射並且如果公式C可以推導自公式A和B，通過推論規則r，就是說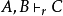，則有某個自然數的算術函式g_r使得 。

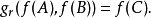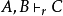
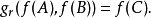
接著，因為這個形式系統是形式算術的，它能做關於數和它們相互的算術聯繫的陳述，可以得出這個系統也可以通過哥德爾編號的方式，間接的做關於自身的陳述: 就是說，形式系統的一個命題可以做出斷言，在從哥德爾映射的角度查看的時候，能轉換成關於同一個形式系統的其他命題，甚至是自身的斷言。所以，通過這種方式一個形式算術可以做關於自身的斷言，而成為自引用的，就像二階邏輯。這提供給哥德爾(和其他邏輯學家)一種探索和發現關於形式系統的一致性和完備性性質的一種方法。

例子

哥德爾數是參照命題演算和形式算術的符號而構造的.每個符號都被指派了一個自然數:

邏輯符號	數 1:12
	1 ("非")
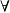	2 ("所有")
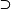	3 ("如果-那么")
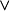	4 ("或")
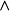	5 ("與")
(	6
)	7
S	8 ("後繼")
0	9
=	10
+	11
×	12
P	15
Q	18
R	21
S	24
v	13
x	16
y	19
E	14
F	17
G	20

以此類推

算術陳述/語句被參照素數系列指派唯一的哥德爾配數。這基於一種簡單的編碼，它在本質上理解為
素數1* 素數2* 素數3
以此類推。 例如陳述
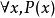變成了2* 3* 5* 7* 11* 13，因為{2, 3, 5, 7, 11, ...} 是素數系列，而 2, 16, 12, 6, 16, 7 是有關的字元代碼。這是個巨大但完全確定的數(14259844433335185664666562849653536301757812500)。

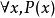
注意通過算術基本定理，這個天文數字可以被分解到唯一的素數因數中；所以轉換哥德爾數回它的字元序列是可能的。

如果我們將此表的"非"指派為二，"所有"指派為一，這樣可以建立另一種哥德爾編碼，但是每個字元序列的哥德爾數仍舊是唯一的。