基本介紹
- 中文名:哈夫曼樹
- 結構:樹形結構
- 算法:哈夫曼算法
- 類別:數據結構
- 發明者:馮·哈夫曼
- 發明國家:德國
- 使用思想:回溯
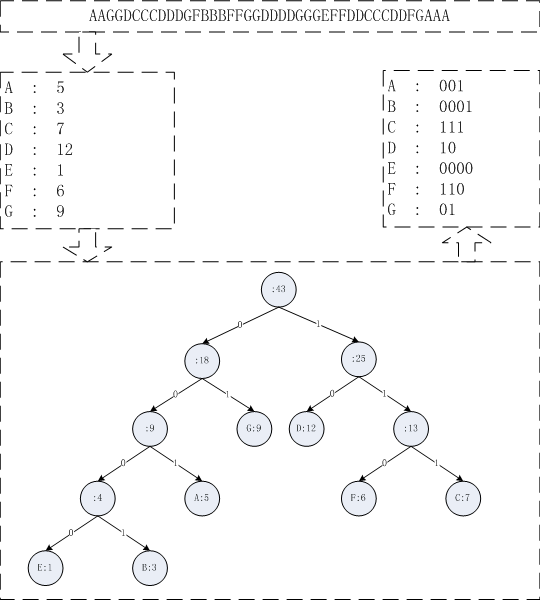
哈夫曼樹是一種樹形結構,用哈夫曼樹的方法解編程題的算法就叫做哈夫曼算法。樹並不是指植物,而是一種數據結構,因為其存放方式頗有點象一棵樹有樹叉因而稱為樹...
哈夫曼編碼(Huffman Coding),又稱霍夫曼編碼,是一種編碼方式,哈夫曼編碼是可變字長編碼(VLC)的一種。Huffman於1952年提出一種編碼方法,該方法完全依據字元出現機率...
哈夫曼樹又稱最優二叉樹,是一種帶權路徑長度最短的二叉樹。所謂樹的帶權路徑長度,就是樹中所有的葉結點的權值乘上其到根結點的路徑長度(若根結點為0層,葉...
給定N個權值作為N個葉子結點,構造一棵二叉樹,若該樹的帶權路徑長度達到最小,稱這樣的二叉樹為最優二叉樹,也稱為哈夫曼樹(Huffman Tree)。哈夫曼樹是帶權路徑...
哈夫曼編碼是一種最優的前綴編碼技術,然而其存在的不足卻制約了它的直接套用。首先,其解碼時間為O(lavg), 其中lavg為碼字的平均長度;其次,更為最重要的是,...
霍夫曼編碼(Huffman Coding)是一種編碼方式,是一種用於無損數據壓縮的熵編碼(權編碼)算法。霍夫曼編碼(英語:Huffman Coding),又譯為哈夫曼編碼、赫夫曼編碼,是一...
適應性哈夫曼編碼(Adaptive Huffman coding),又稱動態哈夫曼編碼(Dynamic Huffman coding),是基於哈夫曼編碼的適自適應編碼技術。它允許在符號正在傳輸時構建代碼,...
最簡哈夫曼樹是一種數據結構,是由德國數學家馮·哈夫曼發現的,又稱最優二叉樹,是一種帶權路徑長最短的樹。...
壓縮算法(compaction algorithm)是指數據壓縮的算法,在電子與通信領域也常被稱為...常見的熵編碼有行程碼(RLE)、LZW編碼、香農(Shannon)編碼、哈夫曼(Huffman)編碼...
4.4.2構造哈夫曼編碼93 9.1.2KMP算法255 4.4.3哈夫曼算法的正確性95 9.1.3Rabin Karp算法258 4.5單源最短路徑96 9.1.4多子串搜尋與AC自動機260 4.5.1算法...
4.2 貪心算法的基本要素4.2.1 貪心選擇性質4.2.2 最優子結構性質4.2.3 貪心算法與動態規劃算法的差異4.3 最優裝載4.4 哈夫曼編碼...
圖論算法在計算機科學中扮演著很重要的角色,它提供了對很多問題都有效的一種簡單...十一、輸入一段文章,全部用小寫字母,求各字母的哈夫曼編碼。十二、要給n個人...
3.4習題第4章貪心算法4.1背包問題的貪心算法4.2求最小生成樹的Kruskal算法4.3求最小生成樹的Prim算法4.4求單源最短路的Dijkstra算法4.5哈夫曼編碼4.6習題...
4.2.3貪心算法與動態規划算法的差異894.3最優裝載914.4哈夫曼編碼924.4.1前綴碼934.4.2構造哈夫曼編碼934.4.3哈夫曼算法的正確性95...
7.3.2遍歷算法探究/1867.4線索二叉樹/1897.5樹和森林/1927.5.1樹的存儲結構/1927.5.2二叉樹與森林/1947.5.3樹和森林的遍歷探究/1957.6哈夫曼樹/196...
《Java數據結構和算法》(第2版)介紹了計算機編程中使用的數據結構和算法,對於在...哈夫曼(Huffman)編碼小結問題實驗編程作業第9章紅-黑樹第10章2-3-4樹和外部...
《數據結構及套用算法》是2008年中國科學技術大學出版社出版的圖書,作者是顧為兵...6.6 哈夫曼樹和哈夫曼編碼6.7 本章小結第七章 圖7.1 圖的基本概念7.2 ...
在數學和計算機科學之中,算法(Algorithm)為一個計算的具體步驟,常用於計算、數據...按照圖論的算法進行分類,算法可以分為哈夫曼編碼、樹的遍歷、最短路徑算法、最...
通過實例說明各種結構在運算操作時的動態特性,並結合典型套用問題給出算法設計與...5.6.3哈夫曼樹的套用1275.7套用實例——並查集129本章小結132習題5133...
7.1 算法思想7.2 任務選擇問題7.3 背包問題7.4 哈夫曼編碼問題7.5 快取維護問題7.6 任務選擇問題實驗7.7 小結習題實驗題第8章 圖算法...
5.2 圖問題中的貪心算法675.2.1 單源最短路徑問題: Dijkstra算法675.2.2 最小生成樹問題: Prim算法和Kruskal算法705.2.3 哈夫曼樹745.3 組合問題中的...
7.2哈夫曼編碼 7.3拓撲排序 7.4最小生成樹 7.4.1 Kruskal算法 7.4.2 Prim算法 7.5汽車加油問題 思考題 第8章分治算法 8.1二分查找 8....
這種方法能夠實現比眾人皆知的哈夫曼算法更好的壓縮,並且它本身非常適合於自適應數據壓縮,自適應數據壓縮的預測與上下文密切相關。算術編碼已經用於二值圖像壓縮標準J...
