吸附速度是指單位時間內單位重量的吸附劑所吸附的量。是衡量吸附處理過程中吸附效果的主要指標之一。吸附速度越快，則達到吸附平衡的時間越短，吸附設備越小。吸附速度主要由吸附質顆粒的外部擴散(膜擴散)速度和內部擴散速度來控制，與吸附劑和吸附質的顆粒大小、表面積、結構有關，也與溶液的攪動程度、溫度等因素有關。
基本介紹
- 中文名：吸附速度
- 外文名：The adsorption rate
- 定義：單位時間單位重量的吸附劑吸附量
- 功能：衡量吸附處理過程中吸附效果
- 特點：吸附速度愈快
- 因素：吸附顆粒速度，攪動程度、溫度
簡介,吸附速度的理論分析,吸附速度理論模型的推廣,對吸附速度的理解,
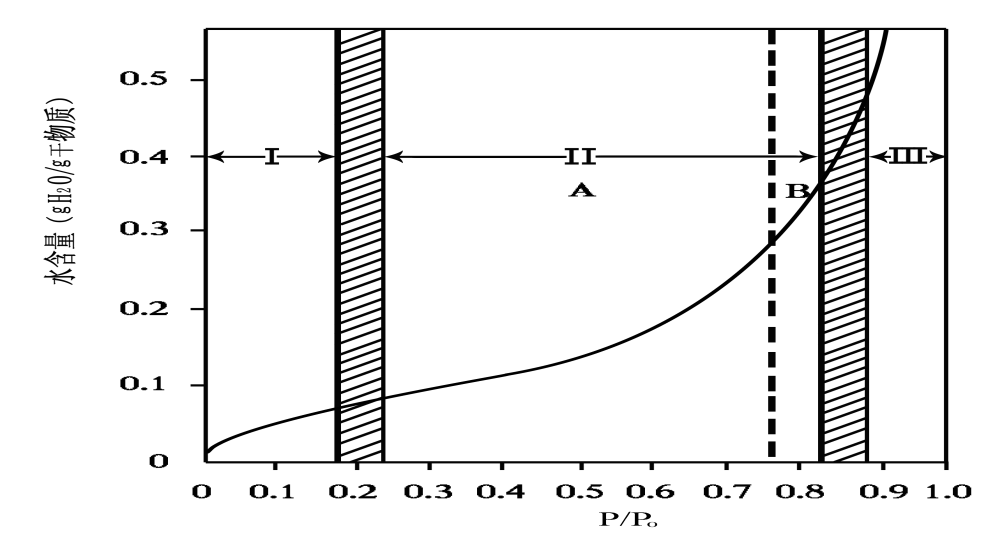
簡介
利用質量傳遞微分方程 ,根據多孔顆粒的邊界條件建立了理論模型，推導出了多孔顆粒的吸附速度方程，並以水工質對為例，對其正確性進行了驗證；同時，從機理上確定了傳質係數 K與相關的各參數之間的函式關係，求出了該方程中的參數ε的函式表達式。由於吸附的情況是多種多樣的，很難 用一個簡單的理論來描述，因而許多理論模型被陸續提出。同時，人們也對複雜的多孔顆粒動態吸附過程給出了許多不同的解釋。
吸附速度的理論分析
吸附劑在流體中吸附物質的速度，可以分為以下3種，其中最慢的起控制作用吸附劑周圍流體界膜內組分物質的遷移速度；吸附劑顆粒內被吸附組分的擴散速度；吸附劑內部表面上的吸附反應速度。試樣為球形顆粒，半徑為R；顆粒外表面壓力P在擴散過程中保持不變；顆粒內部溫度T分布均勻，且在擴散過程中保持不變；擴散過程遵循 Arrhenius 關係，擴散係數在某 一瞬時沿徑向保持不變；顆粒內部無化學反應；擴散在停滯介質中進行，即吸附劑不動；顆粒內部的多孔結構是均勻的，吸附質的濃度僅沿徑向變化，且外表面的吸附質的濃度保持不變；擴散開始時，顆粒內部的吸附質濃度分布均勻。
吸附速度理論模型的推廣
對多孔吸附顆粒在非穩態情況下的傳質速度進行求解。當非平衡吸附過程進行的比較緩慢時，可以對吸附過程作如下的近似處理的曲線為一任意製冷過程中，當量半徑為R的吸附劑所含吸附質的變化曲線。在時刻1的狀態參數分別為:溫度7、壓力P吸附量。若計算步長為△r，在前一步長點吸附質在吸附劑內的比率為。則假想以點1為原點，將過程1-2之間的曲線放大便可得到一個模型圖。當△r足夠小時，作為近似處理，可以認為點2由點1經等溫過程得到的。並假設在點1處，顆粒內濃度分布均勻。這樣，可以對吸附過程進行求解。
對吸附速度的理解
利用質量傳遞微分方程，通過理論推導得出了吸附速度方程的一般式，同時，從機理上確定了傳質係數K與相關的各參數之間的函式關係，吸附速度方程中的參數e並非常數。利用近似的方法得出了方程中參數ε的簡單函式表達式，從而為實際系統模擬中進行吸附速度的準確計算奠定了基礎。當非平衡吸附過程進行的比較緩慢時，可以利用該e的簡單函式表達式，對吸附過程的吸附速度進行求解。
