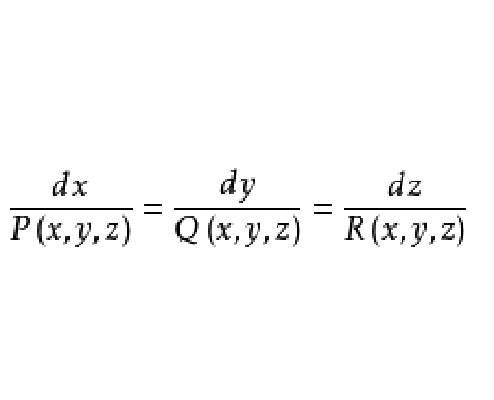向量線

向量線(vector line)是向量場中具有特定意義的曲線，指其切線方向與場中向量一致的向量場中的曲線。設f是定義在區域Ω⊆R上的向量場，Γ是Ω中的光滑曲線，若Γ上每一點處的切向量的方向與f在該點的方向一致，則Γ稱為場f的向量線。例如勢場f的向量線是它的勢函式的梯度線，即這個勢函式變化最快的線。若f是穩定流動(即與時間無關)的流體的速度場，則它的向量線是流體質點的移動軌跡，稱為流線，若f是引力場，則相應的向量線稱為力線。

基本介紹

• 中文名：向量線
• 外文名：vector line
• 所屬學科：數學
• 所屬問題：數學分析(積分學)
• 舉例：靜電場的電力線、磁場的磁力線等
• 相關概念：向量場，切線，場向量等

基本介紹

我們知道，在穩定流動的流體中，質點的瞬時運動方向是該點的速度方向，這就是說，流體中質點的運動軌跡的切線方向，就是速度方向，這條軌跡稱為流線。這就是一般向量場中的向量線概念。

設

為向量場， 為 中的一條曲線。若 上的每一點處的切線方向都與場向量在該點的方向一致，則稱 為向量場 的向量線。靜電場中的電力線、磁場中的磁力線等都是向量線的實際例子。

向量線的方程

設為向量線上任一點，則其矢量方程為

那么

就是向量線在點處的切向量。由定義，它與在點處的場向量共線，因此

這就是向量線所滿足的方程，如果解出它的話，一般就得到向量線族。如果再利用過點這個條件，就得到過點的向量線。一般來說，向量場中每一點有一條且僅有一條向量線通過它，向量線族充滿了向量場所在的空間。

例1由電磁學中的Coulomb定律，在位於原點的點電荷q(這裡q表示電荷大小)所產生的靜電場中，任何一點處的電場強度為

其中為點到原點的距離，，為真空介電常數。

將E具體寫出來就是

由於

所以

1.設S是以原點為心，R為半徑的球面，定向取外側。注意到在球面S上恆有，且E的方向與球面S的外法向量的方向相同，因此從內部穿出球面S的通量(稱為電通量)為

2. 設為任意一張光滑或分片光滑的封閉曲面。

(i) 如果內不含原點。記所包圍的區域為，則由Gauss公式得

(ii) 如果內含有原點，那么不能直接用Gauss公式。在曲面所包圍的區域內取一個以原點為心的小球面，定向取內側。記為介於與之間的區域。由Gauss 公式得

因此從內部穿出曲面的電通量

因此，電場強度穿出任一封閉曲面的電通量等於其內部的電荷量除以，這正是電磁學中的Gauss定律。

此外，利用前面的討論，電場強度的向量線(即電力線)應滿足關係式

由此解得電力線的方程為

這是一族從坐標原點出發的半射線(見圖1)。

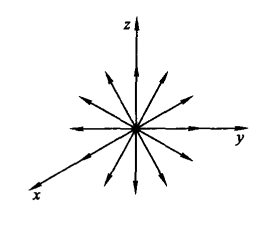
圖1