各向同性張量是指在坐標變換後分量數值即在新老坐標系中保持同名分量相等的張量。或者每一分量都是坐標系做剛體轉到變換下的不變數,則此張量是各向同性張量。
基本介紹
- 中文名:各向同性張量
- 外文名:isotropic tensor
- 性質:分量不因坐標系的旋轉而改變
- 特性:置換定理
- 套用:流體力學等
- 所屬學科:力學
簡述
定義
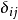


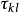

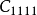


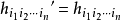
置換定理

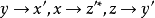
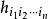

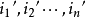
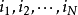
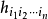
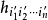
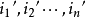
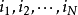
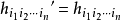
性質
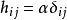
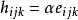


各向同性張量是指在坐標變換後分量數值即在新老坐標系中保持同名分量相等的張量。或者每一分量都是坐標系做剛體轉到變換下的不變數,則此張量是各向同性張量。
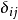


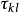

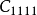


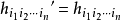

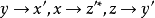
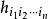

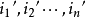
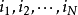
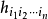
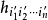
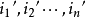
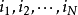
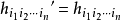
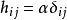
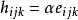

各向同性張量是指在坐標變換後分量數值即在新老坐標系中保持同名分量相等的張量。或者每一分量都是坐標系做剛體轉到變換下的不變數,則此張量是各向同性張量。...
4.1 張量函式4.2 各向同性張量函式4.3 張量函式的導數和微分4.4 Leibniz法則和鏈式法則4.5 張量場絕對微分習題第5章 曲線坐標5.1 曲線坐標系...
4.各向同性張量5.張量的微分運算附錄二熱力學概述1.熱力學研究的對象2.熱力學第一定律,內能3.熱力學第二定律,熵4.勒讓德(Legendre)變換...
5.5.3 各向同性損傷等效應力張量5.6 應變等價原理第6章 連續介質熱力學基礎——不可逆熱力學6.1 熱力學狀態變數6.2 連續介質損傷力學基本守恆律...
1.10張量的極分解25 1.11張量函式27 1.12各向同性張量函式30 第2章運動和變形33 2.1物體的運動33 2.2變形陡度35 [2] 2.3變形陡度的極分解36 2.4應變38 2....
1.5.6 張量的微分運算 1.5.7 各向同性張量 習題 第2章 流體力學基本概念 2.1 流體力學研究的對象、方法及其套用 2.1.1 流體力學研究的對象 2.1.2 流體力學...
1.2.5 各向同性張量 1.2.6 二階張量特性 1.3 張量場及其微分運算 1.3.1 張量場 1.3.2 張量場的不變函式與偏微分方程協變性 1.3.3 微分形式與反對...
各向同性張量函式的倒數中國科學 G輯 2006;36(1):89-102.[20] 王正道, 王溫泉. Bi系2223高溫超導帶材力學性質. 低溫工程 2006;149:54-59....
1.2.5 各向同性張量 1.2.6 二階張量特性 1.3 張量場及其微分運算 1.3.1 張量場 1.3.2 張量場的不變函式與偏微分方程協變性 1.3.3 微分形式與反對...
