基本介紹
- 中文名:反對稱變換
- 外文名:anti-symmetric transformation
- 所屬學科:數學
- 所屬問題:高等代數(歐幾里得空間)
- 簡介:一種線性變換
基本介紹


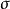
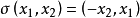
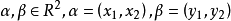



反對稱變換的性質
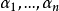
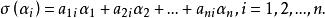


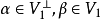
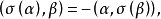


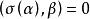


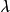
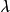


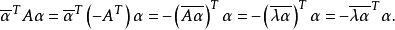


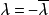
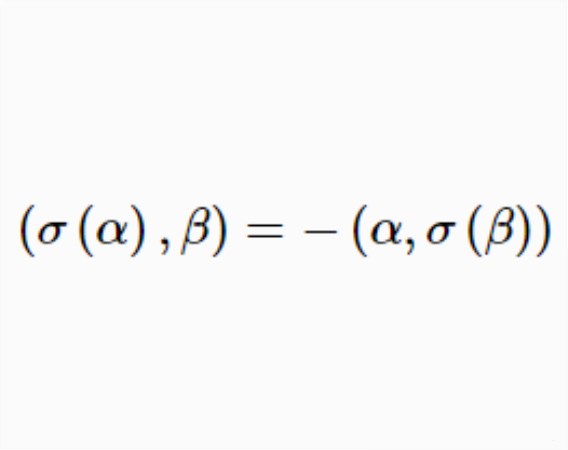


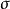
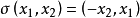
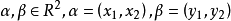



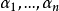
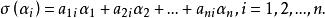


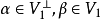
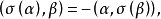


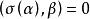


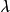
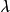


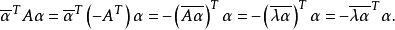


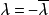
反對稱變換(anti-symmetric transformation)是一種線性變換,設V是歐氏空間,σ是V的線性變換,若對任意α,β∈V,有(σ(α),β)=-(α,σ(β)),則稱σ為V的...
若一個平面圖形K在平面剛體運動m的作用下仍與原來的圖形重合,就說K具有對稱性,m叫做K的對稱變換。對稱變換一般分為:關於X軸或Y軸對稱、關於某一點對稱、關於某...
反對稱約束指分析對象的幾何形狀、邊界條件、材料屬性關於某個面對稱,而載荷關於該面反對稱,並稱該面為反對稱面。該面上的節點滿足法向旋轉為零,切向位移為零(...
實反對稱矩陣(real antisymmetric matrix)是一種反對稱矩陣,指歐氏空間的反對稱變換在標準正交基下的矩陣,即元素aij都是實數,並且aij=-aji(i,j=1,2,…),n的...
共軛反對稱函式(conjugate antisymmetric function)是指具有共軛反對稱特性的一種頻譜函式,序列的傅立葉變換,通常稱為序列的頻譜函式,如果頻譜函式X(ejω)滿足X(e...
注意,對稱關係不是反對稱關係(aRb且bRa得到b=a)的反義。有些關係既是對稱的...微分方程的對稱是指不改變微分方程的變換,這些對稱的知識有助於微分方程的求解。...
伽利略變換伽利略群的中心擴張 編輯 這裡我們只考慮伽利略群的李代數。結果能夠輕易延伸到李群。L的李代數由H、Pi、Ci和Lij張成(反對稱張量),並能夠受交換子的...
物理學關於對稱性探索的一個重要進展是建立諾特定理,定理指出,如果運動定律在某一變換下具有不變性,必相應地存在一條守恆定律。簡言之,物理定律的一種對稱性,對應...
對稱化運算元(symmetrization operator)是作用於反對稱張量上的運算元。張量是向量概念的綜合,可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力...
對稱張量是各分量關於指標對稱的張量,表示r階反變張量全體。x是對稱張量的充分必要條件是它的分量關於各指標是對稱的,x是反對稱張量的充分必要條件是它的分量關於...
在量子力學中,量子系統中的粒子存在運動上反演的性質,稱為時間反演對稱性。對於時間反演對稱性,對應著存在反么正算符。反么正算符即反線性的么正算符。...
