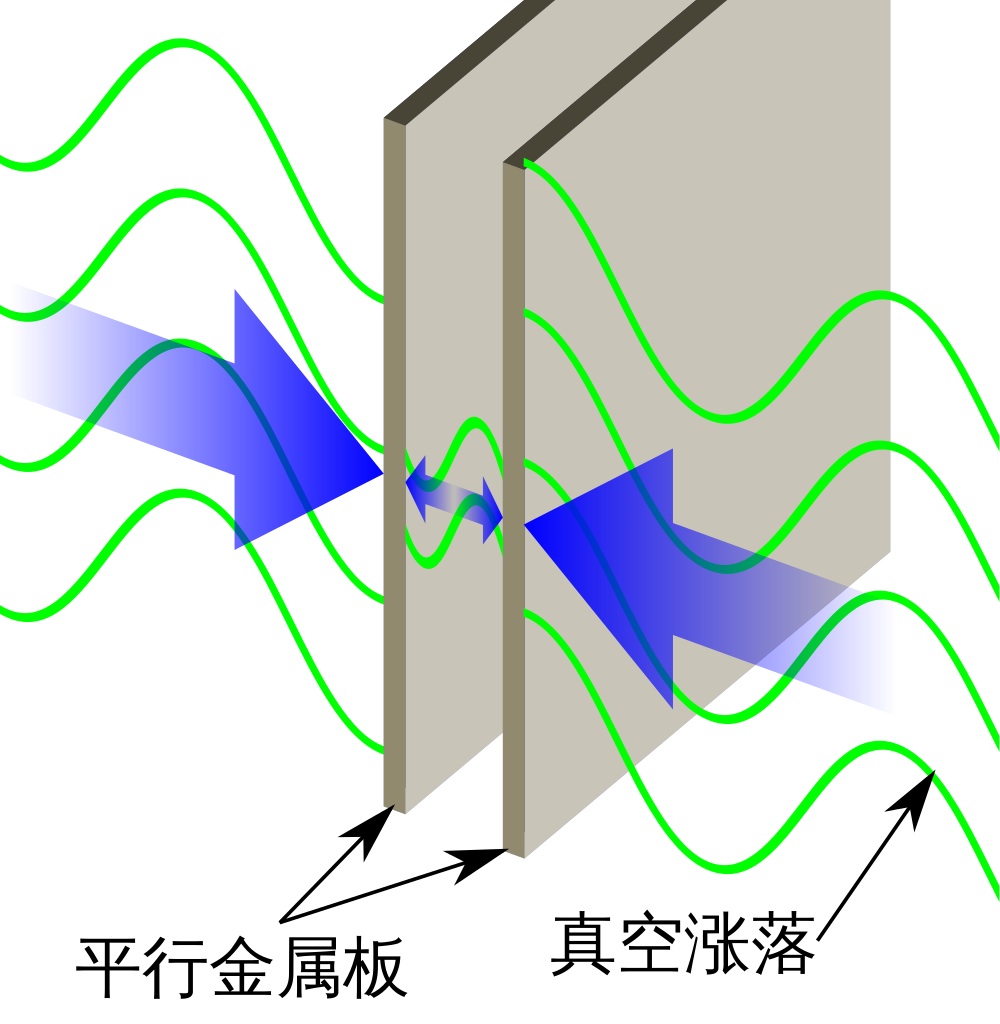
概論 真空能量 卡西米爾效應是
量子場論 的自然結果;量子場論陳述了所有各式各樣的基本
場 —例如
電磁場 —必須在
空間 中每個點且處處被
量子化 。采單純的觀點來說,物理場可以想作是充滿空間的
振動 球 ,之間以
彈簧 相連線。場的強度可以看作是球偏離其平衡位置的位移。場的振動可以傳播,並由對應於此特殊場的適當波方程所主導。量子場論的
二次量子化 程式要求球與彈簧的組合是呈現量子化的,也就是說場強度在空間中每一點被量子化。正則式地(Canonically)來說,空間中每點的場是個
諧振子 ,量子化則成了每點有個
量子諧振子 。場的
激發 則對應到
粒子物理學 中的
基本粒子 。然而,這樣的圖像會顯示出:即使是
真空 也有極其複雜的結構。所有量子場論的計算都須與這樣的真空模型有所關聯。
真空因此暗地裡具有了一顆粒子所擁有的全部性質:
自旋 ,或
光 的
極化 ,以及
能量 等等。若作平均,這些性質會彼此相銷而得到零值——真空的“空”是以這樣的概念維持著。其中一個重要的例外是
真空能量 或能量的真空期望值。簡諧振子的量子化過程指出存在有一個最低的能量值,稱作
零點能量 ,此值不為零:
計算 卡西米爾所做的研究是針對
二次量子化 的電磁場。若其中存在一些大塊的物體,可為金屬或介電材料,做成一如經典電磁場所須遵從的
邊界條件 ,這些相應的邊界條件便影響了真空能量的計算。
舉例來說,考慮金屬腔室中電磁場真空期望值的計算;這樣的金屬腔實例如雷達波腔或
微波 波導 。這樣的例子中,正確找出場的
零點能量 的方法是將腔中
駐波 能量加總起來。每一個可能的駐波對應了一種能量值;例如,第n個駐波的能量值是{\displaystyle E
n 。腔室中電磁場的真空期望值則為:
此和是對所有可能駐波的
n 加總起來。1/2的因子反映出被加總的是零點能量(此1/2與
方程 的1/2相同)。以這樣方式寫出,很明顯地和會
發散 ;然而也是可以將它寫成有限值的表示。
特別來說,可能會有人問為何零點能量會和腔室形狀
s 相依?原因是:每個能級 E
n 都和形狀相依,因此應該將能級
以及真空期望值
寫成形狀
s 的函式。再此可以得到一項觀察:在腔室壁上每個點
p 的力等同於壁形狀
s 出現
攝動 時的真空能量變動,這樣的形狀攝動可寫為
,是位置點
p 的函式。因此得到:
此值在許多實際場合是有限的。
原理 大多數人認為,真空是空蕩蕩的。但是,根據
量子電動力學 (一門在非常小的規模上描述宇宙行為的理論),沒有比這種觀點更加荒謬的了。實際上,真空中到處充滿著稱作“零點能”的電磁能,這正是麥克萊希望加以利用的能量。“零點能”中的“零”指的是,如果把宇宙溫度降至絕對零度(宇宙可能的最低能態),部分能量就可能保留下來。實際上,這種能量是相當多的。物理學家對究竟有多少能量仍存在分歧,但麥克萊已經計算出,大小相當於一個
質子 的真空區所含的能量可能與整個宇宙中所有物質所含的能量一樣多。
圖中央為宇宙溫度絕對零度之零點能量真空埸 平行板電容器在輻射場真空態中存在吸引力的現象稱為卡西米爾效應。考慮一個輻射的電磁場,根據
波粒二象性 ,輻射場可以看作是
光子氣 ,而光子氣可看作是電磁輻射場的
簡諧振動 。
電磁場 量子化 後,可把輻射場
哈密頓 寫成二次量子化的形式。
可見對每個振動模式k,都有零點能(真空能)存在,這個結果是引入場量子化後的自然結果。由於
真空能量 的存在可以帶來實驗可觀測的
物理效應 ——卡什米爾效應。考慮一對距離為a的平行板電容器放在輻射場中,邊界條件為:。可見隨平行板距離的增大,所允許的振動模式越多,因此平行板電容器之間由於真空能量的存在而存在一種吸引力——
卡什米爾力 。反之如果認為不存在真空能,則沒有這種力。在具體的計算過程中,由於U(a)的積分(求和)是發散的。為得到收斂的結果,數學上人為地引入一個切斷因子。
理論特點 卡西米爾效應就是在真空中兩片平行的平坦金屬板之間的吸引壓力。這一理論的特別之處是,“卡西米爾力”通常情況下只會導致物體間的“相互吸引”,而並非“相互排斥“。我們不是鐵道專家和列車脫軌研究專家,對兩列火車在北半球,南北方向並列平行距離很近超高速運行,會不會發生相撞沒有發言權。想到火車相撞中的卡西米爾現象,是由於研究“三旋/弦/圈理論”聯想到的。三旋/弦/圈這三個層次,僅是
龐加萊 猜的層展和呈展,也僅是在計算、套用、理解上的一種方便。如此,分別取“三旋”、“
弦論 ”、“
圈量子 ”的中文拼音第一個字母的大寫S、X、Q,簡稱為SXQ理論,它包含了既有環量子三旋理論,又有超弦/M理論,還有圈量子引力理論等所曾主要表達的數學和物理內容。由於有人認為三旋/弦/圈(SXQ)理論難以實驗檢驗,我們研究卡西米爾現象發現,環量子類似一個方板,球量子類似一個方塊,從三維來說,方板有一維是對稱破缺的。但正是這種破缺,使環量子和球量子的自旋如果存在輻射,那么在卡西米爾效應上是可以實驗檢驗。這種類比模型不僅能擴展引力場方程及量子力學方程求解的思路,豐富正、負時空聯絡的幾何圖象,而且聯繫卡西米爾效應中兩塊板之間零點能的量子漲落差異,還可能揭示宇宙物質的起源以及強力、弱力和電磁力等相互作用的秘密。因為如果把引力聯結的兩個星體比作卡西米爾效應中的兩塊板,再把引力場彎曲產生的凹陷圖象分別貼上在兩塊板相對的一面,引力就類似蛀洞的一個洞口與另一個蛀洞的洞口相對這片區域的卡西米爾效應量子漲落產生的拉力強度。原因是,雖然這種拉力強度遠小於星體物質自身的能量密度,但它們已表現出這片區域內的時空彎曲,相對要大於平板外側的時空彎曲,並是這種彎曲產生的拉力。因為按
海森堡 的
不確定性原理 ,所謂真空實際上充滿著許多瞬時冒出又瞬時消逝的基本粒子,這些基本粒子中的一部分將通過時空彎曲的凹面進行傳播,結果這裡的時空彎曲變成一種引力的耦合輻射。這裡
負能量 與
反物質 的區別是,反物質擁有正的能量,例如當電子和它的反粒子正電子碰撞時,它們就湮滅,其最終產物是攜帶正能量的
伽瑪射線 。如果反物質是由負能量構成的,那么這樣一種相互作用將會產生其值為零的最終能量。但不管是哪種情況,最終這裡的引力場時空彎曲輻射差異產生了拉力強度。由此時空彎曲不僅造成類似纖維叢的底流形與纖維的差別,而且也是產生引力和強力、
弱力 及
電磁力 等相互作用區別的根本因素。因此求解引力,主要還是應該從愛因斯坦廣義
相對論 的引力方程入手。
研究進展 卡西米爾效應最吸引人的地方就是真空不空,能量與物質可以相互轉化。經典的卡西米爾效應試驗是將兩片金屬箔放置在很近的位置,當金屬箔之間的距離小於真空中的虛粒子的波長時,長波排除,金屬箔外的其他波就會使靠攏。兩者距離越近,吸引力越大。這已經在1996年為試驗所證實。即將出版的Physical Review Letters上講,Ho Bun Chan(University of Florida)將卡西米爾效應套用到了計算機晶片的設計上。早在2001年,HoBun Chan就設計了一個納米槓桿,將一張極薄的金箔靠近一個極小的金球,當兩者距離<300納米的時候,兩者就會吸引。作用力的大小與距離相關,這樣就可以利用另一端做微觀世界的測力計。
Ho Bun Chan也證明如果將金箔換為矽片,同樣的效應也會發生。因此對計算機晶片的設計也具有指導意義。因為晶片廠會發現當矽片上的元件小到一定尺度,他們就會沾到一起。然而更有意思的是,卡西米爾效應還有可能成為排斥力。根據Lifshitz(也就是Landau的
理論物理學 講義的合作者)如果將金屬箔和真空換為適當的物質和液體,吸引力就可以變為排斥力。
哈佛大學 的Capasso博士正帶領他的小組在向這個方向努力。因為如果這種天然的排斥力可以形成,我們就可以製造沒有摩擦力的微觀軸承了。





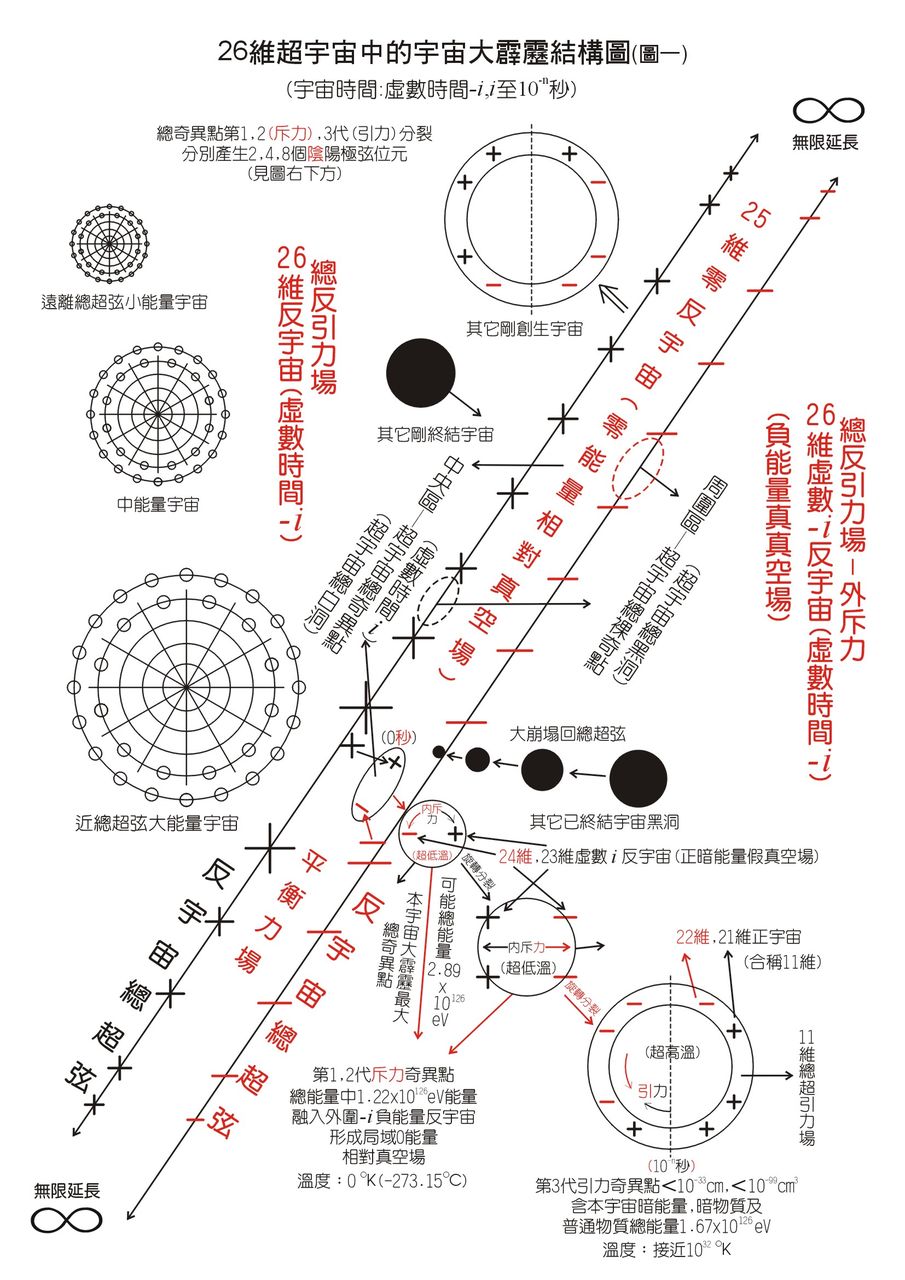 圖中央為宇宙溫度絕對零度之零點能量真空埸
圖中央為宇宙溫度絕對零度之零點能量真空埸