基本介紹
- 中文名：二次量子化
- 外文名：second quantization
- 定義：對量子力學的一種新的數學表述
- 特點：量子力學中，粒子可產生和湮滅
- 研究領域：量子力學
- 性質：數學表述
簡單介紹,對稱化的基矢,正交歸一化關係和完全性關係,提出,研究動機,二次量子化步驟,缺點,
簡單介紹
量子力學基本原理指出，描寫全同粒子系統的態矢量，對於任意一對粒子的對調來說必須是對稱的（玻色子系統）或反對稱的（費米子系統）。全同粒子系統的理論具有很多獨有的特點,人們根據這些特點發展了一種特殊的理論形式，這種使用產生算符和消滅算符在對稱化的希爾伯特空間處理全同粒子系統的方法，通常稱為二次量子化方法。
對稱化的基矢
全同粒子系統的最主要的特點是粒子的不可分辨性，即粒子不可以區分、不可以編號。但是為了作數學上的描述，粒子又必須編號。在對態矢量的模仿中，具有不同號碼的粒子完全處於相同的地位，這樣粒子雖然編了號，但仍是不可分辨的目的。
可以把對稱化和反對稱化的基矢寫成下式的形式，並統稱之為對稱化基矢。
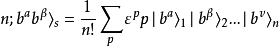
只需對玻色子取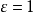
，對費米子取
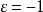即可。這一基矢描寫的是在n個粒子中，有一個處於
態，一個處於
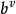態的狀態。由於已經對稱化（以後用對稱化一詞兼代表反對稱化），粒子的編號已無物理意義，因此左邊的基矢符號中不出現粒子的編號。
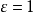
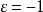
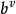
正交歸一化關係和完全性關係
正交歸一化關係和完全性關係即稱化基矢的正交歸一化關係。根據這個關係，不同的基矢是正交的，但一個基矢與自己的內積並不全等於1，對於連續譜也不全等於
函式，而有時是函式再乘一個常數。目前我們不想改變這個情況，因為一律改成1或函式反而不便。這種情況仍稱之為歸一化。
提出
狄拉克曾把麥克斯韋的光關進一個盒子裡，於是光的動態像一組振子。然後他給這種振子強加上量子性質。麥克斯韋的光理論是個波動理論，新的量子化理論實際上是包含波動和微粒兩方面的一個理論，實際上指成群的光子。狄拉克的光理論的成功激發了人們的探索。海森堡和泡利.約爾當和魏格納以及其他人，開始推廣這個見解，把它套用到別的種類的波上，如薛丁格波和狄拉克電子波。雖然這兩種波是量子波，它們既代表純粹的波也代表粒子，但是想要修改這兩種波是有充分理由的。所以理論家取各種各類的量子物質波，其中有狄拉克的電子波，將它看成仿佛是和麥克斯韋光波同等的“經典波”，用一種和狄拉克用於光波的手法原則上類似的手法，給物質波再強加上一些量子性質——這個程式稱作二次量子化。
研究動機
在多體系統中，對於處理全同粒子（identical particles），包括玻色子（bosons）和費米子（fermions）來說，理論上可以用Schrondinger方程去描述這系統。而波函式是各粒子位置或容間的波函式，玻色子和費米子都有相應的方法寫出其波函式而符合其統計條件的。可是，處理這樣的波函式太麻煩，而且若量子態的分布是連續的，處理起來十分麻煩。
因此，研究二次量子化，用升降算符（creation and annihilation operators）去描述，這樣數學處理便容易得多，我們也知道怎樣用這些算符去推演其他可觀察物理量。另外，降算符相干態可用複數（玻色子）或Grassmann數（費米子）表示，數學工具都很齊備。
