卡塔朗數

卡塔朗數(Catalan number)是一個組合數，一些組合計數問題可以歸結為解下列形式的遞歸關係：u_n=u₁u_n-1+u₂u_n-2+…+u_n-1u₁，n≥2，且u₁=1，它的解u_n稱為卡塔朗數。一般認為這種數是由比利時數學家卡塔朗(E.C.Catalan，1814-1894)在1838年首先提出的，但後來有人指出，實際上大數學家歐拉早在1758年就已認識到它了。我國內蒙古師範大學羅見今副教授以大量的史料論證，所謂“卡塔朗數”的首創者其實並非歐洲人，而是我國清朝的蒙古族學者明安圖(1692～1763)。他的發現早於歐拉，比卡塔朗的發現，幾乎早了一百年。

基本介紹

• 中文名：卡塔朗數
• 外文名：Catalan number
• 所屬學科：數學（組合學）
• 簡介：一個組合數

基本介紹

卡塔朗數是一個組合數，一些組合計數問題可以歸結為解下列形式的遞歸關係：u_n=u₁u_n-1+u₂u_n-2+…+u_n-1u₁，n≥2，且u₁=1，它的解為

u_n稱為卡塔朗數，它的生成函式是

解下列這類問題都能得到卡塔朗數：

1.把一個凸n+1邊形用n-2條對角線將它分成互不重疊的三角形，這種分法的總數為u_n；

2.用n條互不相交的弦連結圓周上2n個點的不同方式總數為u_n+1；

3.有n個端點(根點除外)的3階平面植樹的個數為u_n；

4.n個元a₁，a₂，…，a_n不改變順序組成連乘積，可以用n-1個括弧表示相乘的過程，所有不同過程的個數是u_n；

5.坐標平面上由O(0，0)至點U(2n，0)的路徑，每段由格點(i，j)至(i+1，j+1)或(i+1，j-1)，所有在上半平面內且允許經過x軸上的點、而不許越過x軸的路徑數等於u_n+1；

6.由O(0，0)至U(2n，0)的路徑，但不允許中間經過x軸上的點，共有u_n條。

卡塔朗數的前幾項如下：

u₁=1， u₂=1， u₃=2， u₄=5， u₅=14，

u₆=42， u₇=132， u₈=429，

u₉=1430， u₁₀=4862。

相關分析

公園售票視窗前有2n個人排隊買票，每張門票定價5角，每人限購一張。這些人中，只帶一張5角人民幣的與只帶一張1元人民幣的各有n人。開始售票時，售票視窗沒有角票可以找零。試問：大家都能順利買票，售票員始終沒有找不出零錢困擾的排隊方法共有多少種?

用0代表身邊帶5角錢的人，1代表帶1元錢的人，則本問題即可變成：有n個0和n個1，問有多少種排列方法，使排成的0、1序列里，任意前i(i可從1變到2n)個數字中，0的個數總不少於1的個數，此性質稱為前束性質。如能將問題轉化為圖形，那當然更易了解。為此，我們把0看作向右走一步，把1看作向上走一步，則很明顯，n個0和n個1所組成的序列將和圖中從原點(0，0)到點(n，n)的遞增路徑是一一對應的。於是，我們只要計算路徑的條數就行了。

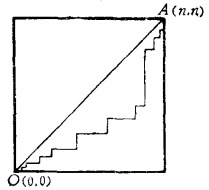圖1

再進一步看問題，具有前束性質的0、1序列正好與不越過對角線OA的遞增路徑一一對應(見圖1)。而這種路徑的條數

其中(n=0，1，2，…)，這就是有名的卡塔朗數，其前十項是1，1，2，5，14，42，132，429，1430，4862。

除了排隊找零票問題可以引出卡塔朗數之外，凸n+1邊形的三角形剖分方法種數(如圖2，這種三角形只能以凸多邊形的邊與對角線為其三邊)以及n個指定了順序的實數的乘積結合方式種數也都可以引出它。據不完全統計，卡塔朗數的各種組合數學的解釋已經不下五十種之多。

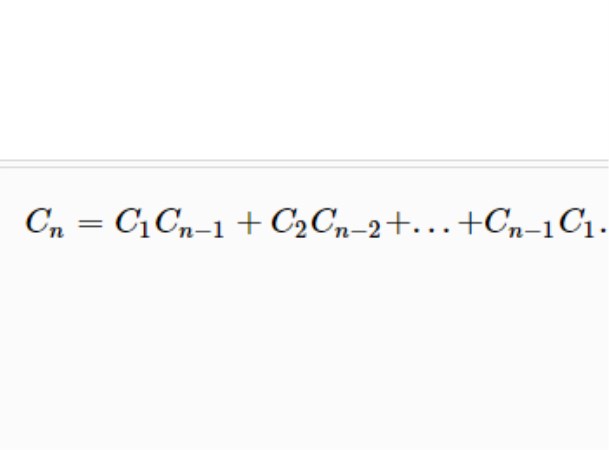
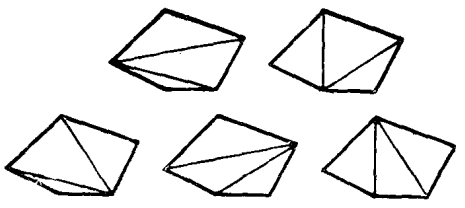圖2 凸五邊形的不同三角形剖分

卡塔朗數還有一個極其直觀的幾何意義，它可以看作是楊輝三角形中“中垂線”上的數除以依次遞增的自然數而得見圖3)。

卡塔朗數有一個簡單而漂亮的遞推公式如下：