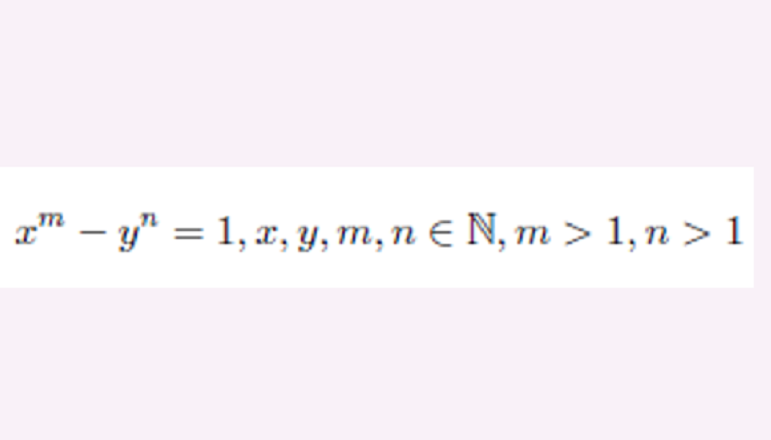設 Z,N,Q 分別表示全體整數,正整數以及有理數的集合。1844 年,Catalan曾經猜測:正整數8和9是唯一的兩個連續的完全方冪。
凱特蘭於1842 年提出:“除了8=2^3,9=3^2以外沒有兩個連續數都是正整數乘冪的猜想”。即不定方程x^p+1=y^q,其中p ,q 均是素數,除了8=2^3,9=3^2 以外沒有其它的正整數解。160 多年來數學家們證明了下列定理:歐拉(Euler)首先證明了不定方程x^2-1=y^q,當q=3 時猜想成立;大約1961 年卡塞爾斯證明了不存在三個相鄰的正整數是完全冪。1962 年柯召證明了當q > 3 時,不定方程x^2-1=y^q 無正整數解。
另外,《數學猜想集》的定理1.3.16 “不定方程x^p+1=y^q,q 是奇素數,沒有x > 0,y >0 的正整數解”。
基本介紹
- 中文名:卡塔朗猜想
- 外文名:Catalan conjecture
- 提出者:Catalan
- 時間:1842年
- 學科:數論
- 解決者:Mihˇailescu
概述,證明,
概述
設 Z,N,Q 分別表示全體整數,正整數以及有理數的集合。1844 年,Catalan曾經猜測:正整數8和9是唯一的兩個連續的完全方冪。顯然,上述猜想可表述為
猜想 1.1 方程
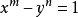
僅有解 (x,y,m,m) = (3,2,2,3)。
這是數論中的一個著名難題,一百多年來人們曾對此有過大量的研究。 例 如,Lebesgue證明了:方程 (1.1) 沒有適合 2|n 的解 (x,y,m,n);柯召證明了:方程 (1.1) 僅有解 (x,y,m,n) = (3,2,2,3) 適合 2|n。 2004 年,這一猜想最終由Mihˇailescu完全解決。
1986 年,Shorey 和 Tijdeman 將 Catalan 猜想擴展到了有理數的範圍,提出了以下猜想:
猜想 1.2 方程
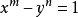
僅有有限多組解 (X,Y,m,n)。
上述猜想稱為廣義 Catalan 猜想。 由於該猜想與著名的廣義 Fermat 猜想有直接的聯繫,所以這是一個很有意義但又非常困難的問題,目前僅解決了一些 極特殊的情況。例如,vander Poorten證明了:對於給定的 S 集合,即由有限多個素數經乘法生產的正整數的集合,方程 (1.2) 僅有有限多組解(X,Y,m,n)可使 X 和 Y 都是 S - 整數,即分母是該 S 集合中元素的有理數。
證明
廣義Catalan 猜想在mn是偶數時的情況
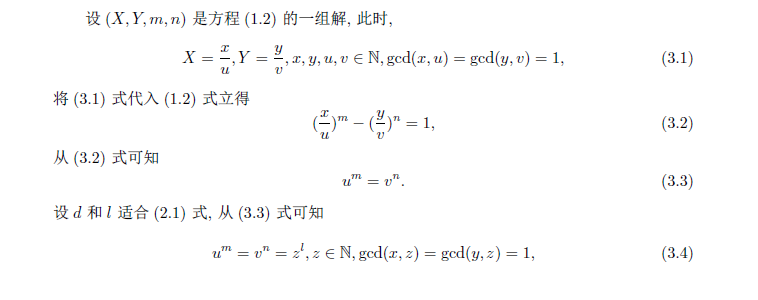


證明:x,y和z中有一數的素因數給定時,該猜想是正確的