卡塔朗定理是一個著名的極值問題。自△ABC內的一點作各邊的垂線,若以各垂線長作成的正方形面積之和為最小,則該點為連結三垂線垂足所成三角形的重心。
基本介紹
- 中文名:卡塔朗定理
- 外文名:Catalan theorem
- 適用範圍:數理科學
簡介,舉例,卡塔朗,
簡介
卡塔朗定理是一個著名的極值問題。
自△ABC內的一點作各邊的垂線,若以各垂線長作成的正方形面積之和為最小,則該點為連結三垂線垂足所成三角形的重心。
舉例
如圖,KD⟘BC,KE⟘AC,KF⟘AB,且KD2+KE2+KF2為最小,則K是垂足△H1H2H3的重心。此點又是原三角形的類似重心。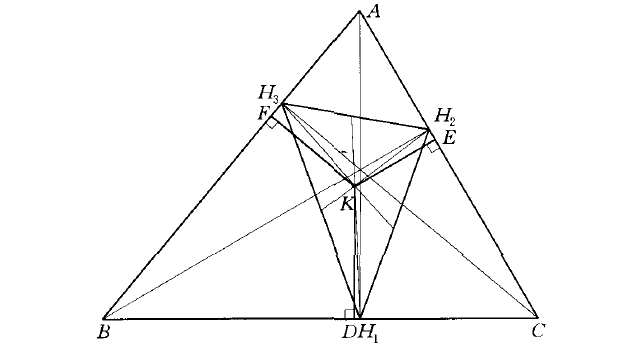 圖1
圖1
 圖1
圖1卡塔朗
卡塔朗一生共發表200多種涉及各數學領域的論著,在微分幾何中,他證明了下列所謂卡塔朗定理:當一個直紋曲線是平面和一般的螺旋面時,它只能是實的極小曲面,他還和雅可比(Jacobi,C.G.J.)同時解決了多重積分的變數替換問題,建立了有關的公式。此外,他還在函式論、伯努利數和其他領域也做出了一定的貢獻。
