在機率論和統計學中,協方差是一種兩個變數如何相關變化的度量,而協方差函式或核函式,描述一個隨機過程或隨機場中的空間上的協方差。
基本介紹
- 中文名:協方差函式
- 外文名:Covariance function
- 領域:統計學
定義

可容許性
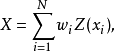

平穩簡化



參見
- 隨機場
在機率論和統計學中,協方差是一種兩個變數如何相關變化的度量,而協方差函式或核函式,描述一個隨機過程或隨機場中的空間上的協方差。

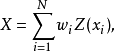




在機率論和統計學中,協方差是一種兩個變數如何相關變化的度量,而協方差函式或核函式,描述一個隨機過程或隨機場中的空間上的協方差。...
馬特恩協方差函式(英語:Matérn covariance function)是統計學中的一個協方差函式,其名稱源於瑞典林業統計學家馬特恩(Bertil Matérn)。...
在統計學中,特定時間序列或者連續信號Xt的自協方差是信號與其經過時間平移的信號之間的協方差。...
對每一類協方差平穩過程 Yt 計算其自協方差序列,如果這個序列 {γj }是絕對可加的,那么一種概括這些協方差的方法是運用一個標量函式,這個函式稱為自協方差生成...
1 定義 ▪ 相關函式 ▪ 相關係數 2 分類 ▪ 1.自相關函式 ▪ 2.互相關函式 ▪ 3.協方差函式 3 性質 4 套用 相關...
自相關函式(Autocorrelation Function)在不同的領域,定義不完全等效。在某些領域,自相關函式等同於自協方差(autocovariance)。自相關(英語:Autocorrelation),也叫序列...
譜分布函式亦稱譜函式,是平穩過程理論的重要概念。譜分布函式 F 不是惟一的,但它們之間最多相差一常數。由相關函式 R(𝜏) 與由協方差函式 𝛤(r) 確定的譜...
在統計學與機率論中,自相關矩陣與自協方差矩陣,互相關矩陣與互協方差矩陣可以通過計算隨機向量(自相關或自協方差時為x,互相關或互協方差時為x,y)其第 i 個...
COVAR函式屬於EXCEL統計函式中的一員,表示為返回協方差,即每對變數的偏差乘積的均值。...
半方差函式(Semi-variogram)及其模型,半方差函式也稱為半變異函式,它是地統計學中研究土壤變異性的關鍵函式。如果隨機函式Z(x)具有二階平穩性,則半方差函式((h)...
以凡,(:)(或幾、(:))表示第7 }J兩個分量的互相關函式(對應地互協方差函式),則在T一(一二,+二)情形,存在(一二,+二)上的有界變差函式F;; ( }),...
它是自相關函式根據平穩序列的有窮樣本的估計量.設{x}}是平穩零均值序列,xi,二:,…,二:是有限樣本觀測值.樣本自協方差函式記為夕*,樣本自相關函式定義為pk=...
若樣本的協方差與其向量的方向無關,即僅與距離有關,則可使用具有各向同性(isotropy)的核函式。很多核函式同時滿足平穩性和各向同性,這裡給出其常見例子 [3] :1...
,各總體的協方差距陣滿足 ,這時線性判別函式為其判別準則為:當 x 落入 內時, ,判 ,其中。當m 個總體 的協方差矩陣 不同時,令則...
Excel函式一共有11類,分別是資料庫函式、日期與時間函式、工程函式、財務函式、...COVAR 返回協方差,即成對偏移乘積的平均數CRITBINOM 返回使累積二項式分布小於等於...
在時間序列分析分析中[1 [1] ],對於時間序列{Xt,x∈T},任取t,s∈T,定義γ(t,s)為序列{Xt}的自協方差函式:γ(t,s)=E(Xt-μt)(Xs-μs)定義ρ(...
主詞條:核函式高斯過程的性質與其協方差函式有密切聯繫,在構造高斯過程時,一些特定形式的協方差函式被稱為核函式。核函式的選擇要求滿足Mercer定理(Mercer's theorem...
力η(t)具有高斯機率分布與自協方差函式(auto-covariance) 力η(t)具有高斯機率分布與自協方差函式 其中kB是波耳茲曼常數和T是溫度。該δ函式在時間上的相關性...
這種結構是用序列的自相關函0,1,…)來描述的,為序列的自協方差函式值,m=Ex(t)是平穩序列的均值。常常採用下列諸式給出m,γ(k),ρ(k)的估計: ,通(k)...
(TEC)值,計算球型格線點上的TEC 值 ;第二種是廣泛套用於地質統計學的基於 Kriging 插入方法,該方法利用已知的樣本值和設定的協方差函式(變差函式)來確定不同...
