基本介紹
- 中文名:區間代數
- 外文名:interval algebra
- 領域:數學
- 性質:特殊的布爾代數
- 對象:線性序集
- 生成方式:線性序擴充而來
代數概念,線性序集,代數公式,代數發展,
代數概念
區間代數(interval algebra)是一種特殊的布爾代數。設L是有首元素OL的線性序集,將L的線性序擴充到L∪{∞},其中∞是不在L中的一個元素,並且規定對每一個x∈L,x<∞.對任意x,y∈L∪{∞},集合[x,y)={z∈L|x≤z<y}稱為L的由x與y決定的半開區間。設A是由L的所有可以表示為有限個半開區間的並的子集所構成的集合,那么A對集合的並、交、補運算構成布爾代數,稱為L的區間代數。當L沒有首元素時也可構成區間代數。布爾代數A同構於一個區間代數若且唯若它由一個鏈CA所生成。
線性序集
線性序集亦稱線性序集。又稱鏈。一類重要的偏序集。若偏序集P適合公理P4:若對任意x,y∈P,x<y,y<x,x=y三式中有且僅有一式成立,則稱P為全序集。全序集中的關係≤稱為全序或線性序。若偏序集P的子集C作為子偏序集是全序集,則稱C是P中的鏈;若C是非序的,則稱C為P的反鏈。實數集及其任何子集在通常的≤關係下是全序集。
設(A,≤)是偏序集,如果(A,≤)中的關係≤滿足條件:對於任意的a,b∈A,a≤b或b≤a至少有一個成立,那么就稱關係≤為序關係,稱A為在這個關係下的全序集(也稱有序集)。
若兩個全序集的元素相同,並且序關係也相同,則稱這兩個全序集是相同的。即:
(A1,≤1)=(A2,≤2)⇔A1=A2且≤1=≤2
當用列舉法表示全序集時,通常規定從左到右表示元素的順序.例如,設N為自然數集,關係≤為平常的數的小於或等於關係,則全序集(N1,≤)表示為{1,2,3,…};若序關係≤定義為:
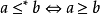
則全序集(N,≤*)表示為{…,3,2,1}
代數公式
又稱“邏輯代數”,是英數學家、邏輯學家布爾(George Boole 1815-1864)所創立的一個代數系統。布爾認為,邏輯關係和某些數學運算甚為類似,代數系統可以有不同的解釋,把解釋推廣到邏輯領域,就可以構成一種思維的演算。他在其著作《邏輯的數學分析》(1847年)及《思維規律》(1854年)中引進了邏輯代數基本概念,構成了一個抽象代數系統。用這種系統可以較容易地處理傳統邏輯所不能處理的邏輯問題。布爾對他的代數系統給了四種解釋:一種是類演算,兩種是命題演算,一種是機率演算。
經過後來數學家的進一步改進,布爾代數成為如下的一個數學系統:設B是一個至少有兩個元素的集合,其中定義兩種運算:+(邏輯加法)。*(邏輯乘法),B中元素對於這兩種運算,如果滿足下面公理:對任意的x,y,z∈B,
公理1:x+y=y+x;x*y=y*x
公理2:x*(y+z)=(x*y)+(x*z)
x+(y*z)=(x+y)*(x+z)
公理3:B中有元素0和1滿足:
x+0=x;x*1=x;
公理4:對任意x∈B,有x′∈B,使
x+x′=1;x*x′=0;則稱B為一個布爾代數。
例如,令B={0,1},讓1表示真命題,0表示假命題,定義+運算如下:
0+0=0;0+0=1;1+0=1;1+1=1;定義*運算如下:
0*0=0;0*1=0;1*0=0;1*1=1;
則它表示的就是一個命題代數系統。由於有1+1=1,它不同於一般的代數系統。
在布爾代數的基礎上,人們又發展了開關代數。開關代數在組合電路、電路網路中有極大的套用價值。
代數發展
布爾代數也屬於一種特殊的代數。布爾(Boole,G.)於1847年及1854年研究思維規律(邏輯學、數理邏輯)時提出的,而它作為一種特殊的格則是由戴德金(Dedekind,J.W.R.)後來提出的.所謂布爾代數,是指一個有序的四元組(B;∧,∨,′),其中B是非空集合,∧和∨分別是B上的二元運算,而“′”是定義在B上的一個一元運算,並且滿足下列條件:對任意a,b,c∈B
1.a∧b=b∧a,a∨b=b∨a.
2.a∧(b∧c)=(a∧b)∧c,
a∨(b∨c)=(a∨b)∨c.
3.a∧(a∨b)=a,a∨(a∧b)=a.
4.(a∧b)∨(b∧c)∨(c∧a)
=(a∨b)∧(b∨c)∧(c∨a).
5.(a∧a′)∨b=b,(a∨a′)∧b=b.
1904年,亨廷頓(Huntington,E.V.)發現:若集合A有一個二元運算∨和一個一元運算 ′,定義a∧b=(a′∨b′)′,並滿足:
1.a∨b=b∨a;
2.a∨(b∨c)=(a∨b)∨c;
3.(a∧b)∨(a∧b′)=a;
則A是布爾代數.這是布爾代數的一個典型結果。1967年、1968年,戈萊茲(Gra¨tzer,G.)和莫肯濟(Mckenzie,R.N.)、塔爾斯基(Tarski,A.)分別獨立地進一步發現布爾代數可僅用一個恆等式來定義。
